Problem statement: You have a list of items that you want to randomize.
I’ve found myself in this situation many times. If the language you’re working in has a shuffle or randomize function, you’re set. However, there are plenty of languages that don’t provide built in support for such a function, leaving you on your own. The first time I was faced with this problem, I wrote a shuffle algorithm that looked something like this:
def incorrect_shuffle(items):
for i in range(len(items)):
randomIndex = random.randint(0, len(items)-1)
temp = items[randomIndex]
items[randomIndex] = items[i]
items[i] = temp
return items
The above algorithm swaps every element in the list with another randomly-chosen element in the list. But there are three problems with this algorithm:
- It’s biased.
- It’s biased.
- It’s biased.
Ok, so there’s really only one problem, but its a big one! This topic has been covered before, most notably by Jeff Atwood in his The Danger of Naïveté post. I’m writing this post to re-emphasize the importance of this topic, especially since I’ve made the mistake of implementing an incorrect shuffle in the past.
How do we know that that above algorithm is biased? On the surface it seems reasonable, and certainly does some shuffling of the items.
There are two ways to realize the incorrectness of the above algorithm. The first is theoretical. A list of N items has N factorial (N!) possible orderings. Consider a list with three elements A, B, and C. There are 3! = 6 ways to order these elements:
ABC ACB BAC BCA CAB CBA
However, the above incorrect algorithm does not yield N! potential orderings. Each item’s final list index is chosen randomly from 0 to N, resulting in N possible final locations for each item. There are N items in the list, so this implementation results in N^N possible orderings. Since N^N is not evenly divisible by N!, some of the final list orderings must be more common than others. This produces a bias for these orderings (e.g., they’re more common than other orderings).
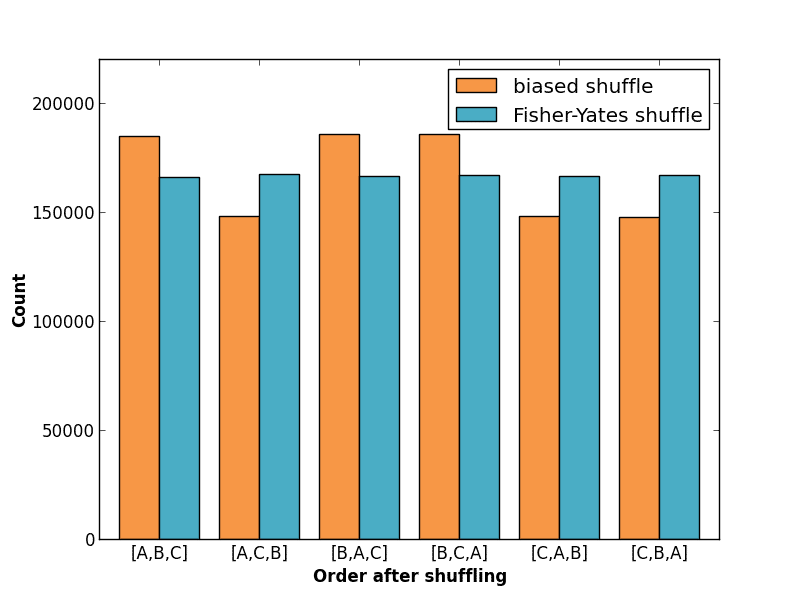
The second way to observe the incorrectness is empirical (e.g., by running some examples). Let’s try to randomize our three element [A,B,C] list with the above biased algorithm, and compare those results to randomizing the list with the Fisher-Yates implementation shown below:
def fisher_yates_shuffle(items):
for i in range(len(items)):
randomIndex = random.randint(i, len(items)-1)
temp = items[randomIndex]
items[randomIndex] = items[i]
items[i] = temp
return items
If we shuffle our [A,B,C] list 1,000,000 times with each algorithm we end up with the following distribution for each of the six possible list orderings:
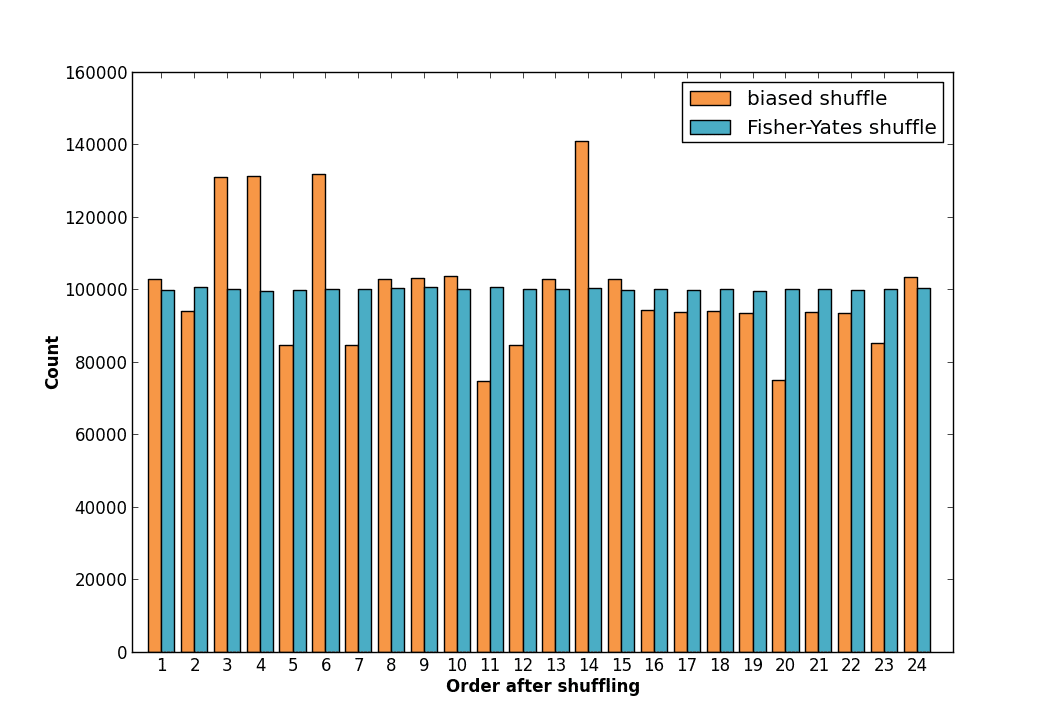
The results show that the biased shuffle produces certain orderings more often than others. The correct Fisher-Yates algorithm produces each outcome with equal likelihood. We can repeat this experiment for a list with four elements. Here are the results:
The numbers 1-24 each represent one of the 24 possible orderings of a list with four elements. The Fisher-Yates shuffle produces each final ordering with equal likelihood. The incorrect algorithm does not.
The first time I saw this I was quite surprised. What makes this problem especially interesting is that the difference between the two algorithms is essentially one character. The incorrect algorithm has the line:
randomIndex = random.randint(0, len(items) - 1)
The Fisher-Yates algorithm uses the following line instead:
randomIndex = random.randint(i, len(items) - 1)
The Fisher-Yates shuffle algorithm (also called the Knuth shuffle) walks a list of items and swaps each item with another in the list. Each iteration the range of swappable items shrinks. The algorithm starts at index zero (it can also walk the list in reverse), and chooses a item from 0 to N at random. This selection freezes the 0th element in the shuffled list. The next iteration moves to index 1 and chooses an item from the remaining 1 to N indices. This repeats until the entire list is walked.
On the surface, using something similar to the incorrect shuffle algorithm might not seem like a big deal. However, the shuffling bias grows as the number of list items grows since N^N grows faster than N!. The Fisher-Yates algorithm is a good one to have in your pocket. It comes in handy more often that you would think.

Why didnt you just implement the following algorithm in the first place?
It is equivalent to popping a randomly chosen item until the input list is empty.
What made you expect that swapping randomly chosen items n times would shuffle the list?
Hi Henri,
Had I known about Fisher-Yates I would have of course used it over the incorrect algorithm :). I found myself in a situation where I needed to randomize/shuffle a collection, and the naive/incorrect implementation certainly does some shuffling, just in a biased way. What I found so interesting is that it’s not immediately obvious that the incorrect algorithm is biased.
Think u have a cut and paste error as both algorithms are the same except for name unless I am hulcinating – which has happened befor
There is a difference in the randomIndex line. The incorrect algorithm has
randomIndex = random.randint(0, len(items) - 1)and the Fisher-Yates implementation has
randomIndex = random.randint(i, len(items) - 1)Yes I noticed right after I hit submit!
This is stated in what you’ve written, but the interesting part about this is that you actually achieve better randomization by reducing the number of outcomes. I wonder if the “naive” algorithm is periodically “more-correct”? That is, when N^N == k*n! then the “overflow” in outcomes produced by the naive algo would, itself, distribute evenly over n! outcomes.
Actually … The number of outcomes isn’t reduced. There *are* only 720 possible combinations for a 6 card deck (6!). The outcome of the naive version however isn’t 6!, but 6^6. Where do these other combinations come out from? They actually don’t. They just repeat the 6! more often and in an uneven way.
Matt actually provided a link to another article on CodingHorror. It’s very well written and explains quite a lot.
You migt want to check it out, if you’re still wondering why Fisher-And-Yates is better than the naive version. ;-)
the example need to be more in explanation and solve a problem.
I don’t get it. I understand the math behind it, I see your graphs, but when I try it myself both shuffles give the same distribution. Run this:
def pstats(f, items, n):
stats = {}
for i in range(n):
shuffled = f(items)
shuffledStr = ”.join(shuffled)
if not shuffledStr in stats:
stats[shuffledStr] = 0
stats[shuffledStr] += 1
import pprint
pprint.pprint(stats)
items = [‘A’,’B’,’C’]
pstats(incorrect_shuffle, items, 240000)
pstats(fisher_yates_shuffle, items, 240000)
sir, i work for a communication industry…and i want to know is there any algorithm to shuffle the data sequence and rearranging it again at the receiver in the correct order without passing the transmitted pattern…….
here in this example you are using random function whose value will be different every time i run that statement….therefore we need to transmit the whole pattern to the receiver so that we may arrange the data at receiver in correct order..
actually is there any method of shuffling or you can say rearranging any sequence without using random function……so that we donot need to transmit the whole new pattern to the receiver…..
it can be generated at the receiver using the same algorithm we used at the transmitter……..
then we donot need to transmit the new pattern….
it will help in reducing bandwidth required for transmission
Thanks for the post!
A question regarding your theoretical explanation: you wrote “this implementation results in N^N possible orderings”. how could it create n^n permutations, if n^n>n! and there exist only n! permutations of an n-elements array?
You are correct that there are only N! permutations for the array. The N^N possible outcomes means that some result orderings will be duplicates. Since N^N is not divisible by N!, it means the some orderings will be duplicated more than others, resulting in the bias for those orderings.