Mean shift clustering is one of my favorite algorithms. It’s a simple and flexible clustering technique that has several nice advantages over other approaches.
In this post I’ll provide an overview of mean shift and discuss some of its strengths and weaknesses. All of the code used in this blog post can be found on github.
Kernel Density Estimation
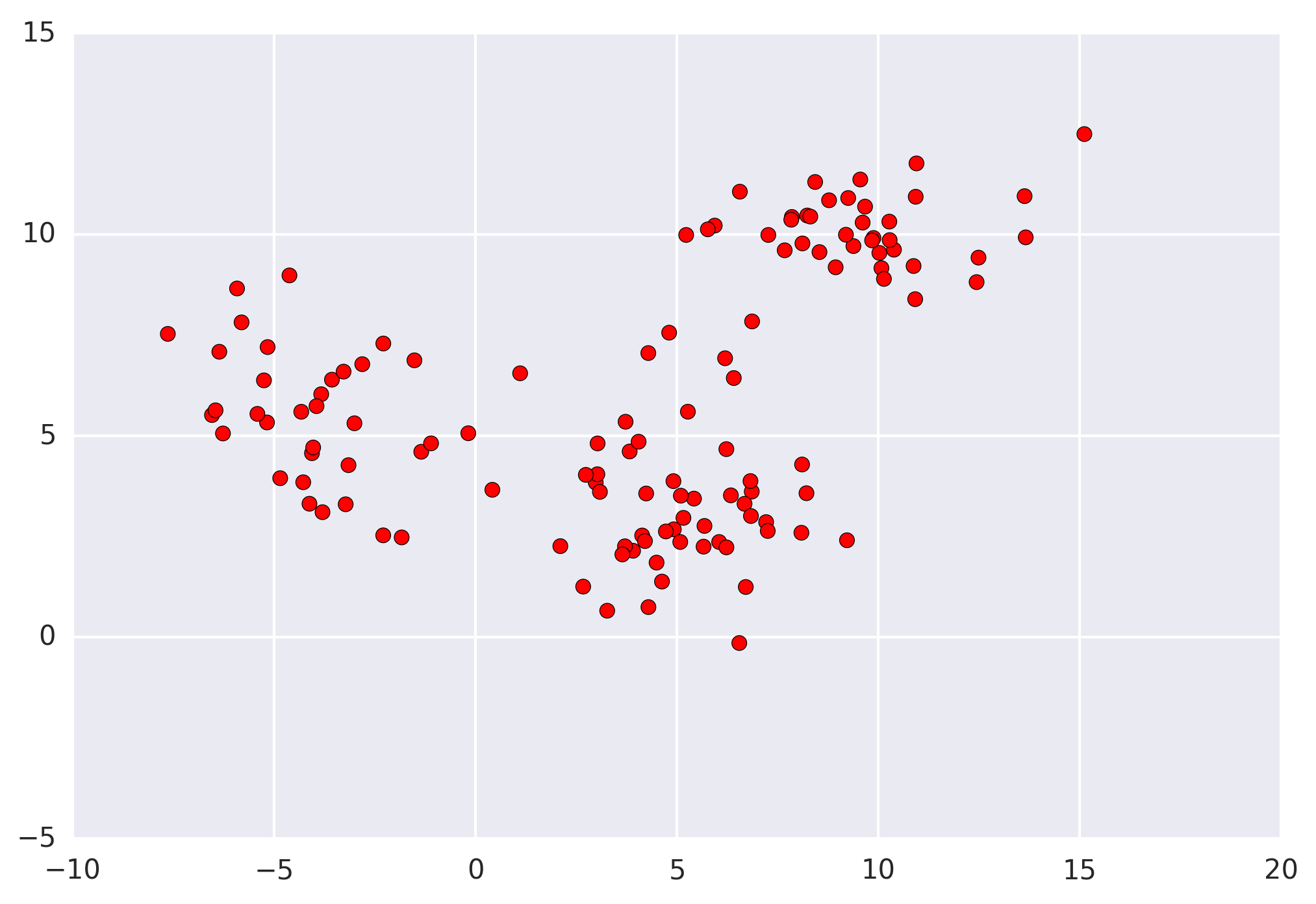
The first step when applying mean shift (and all clustering algorithms) is representing your data in a mathematical manner. For mean shift, this means representing your data as points, such as the set below.
Mean shift builds upon the concept of kernel density estimation (KDE). Imagine that the above data was sampled from a probability distribution. KDE is a method to estimate the underlying distribution (also called the probability density function) for a set of data.
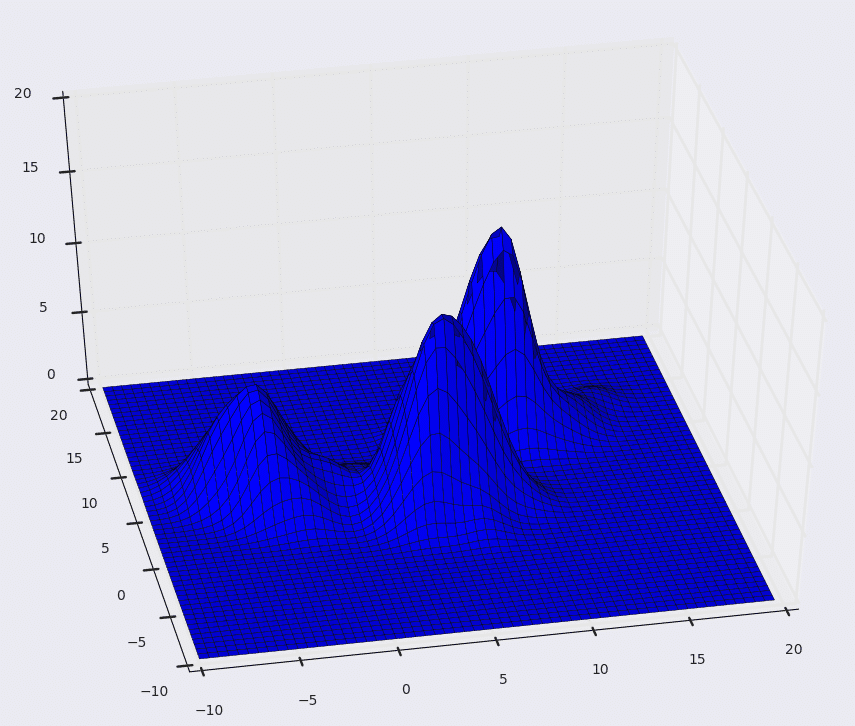
It works by placing a kernel on each point in the data set. A kernel is a fancy mathematical word for a weighting function. There are many different types of kernels, but the most popular one is the Gaussian kernel. Adding all of the individual kernels up generates a probability surface (e.g., density function). Depending on the kernel bandwidth parameter used, the resultant density function will vary.
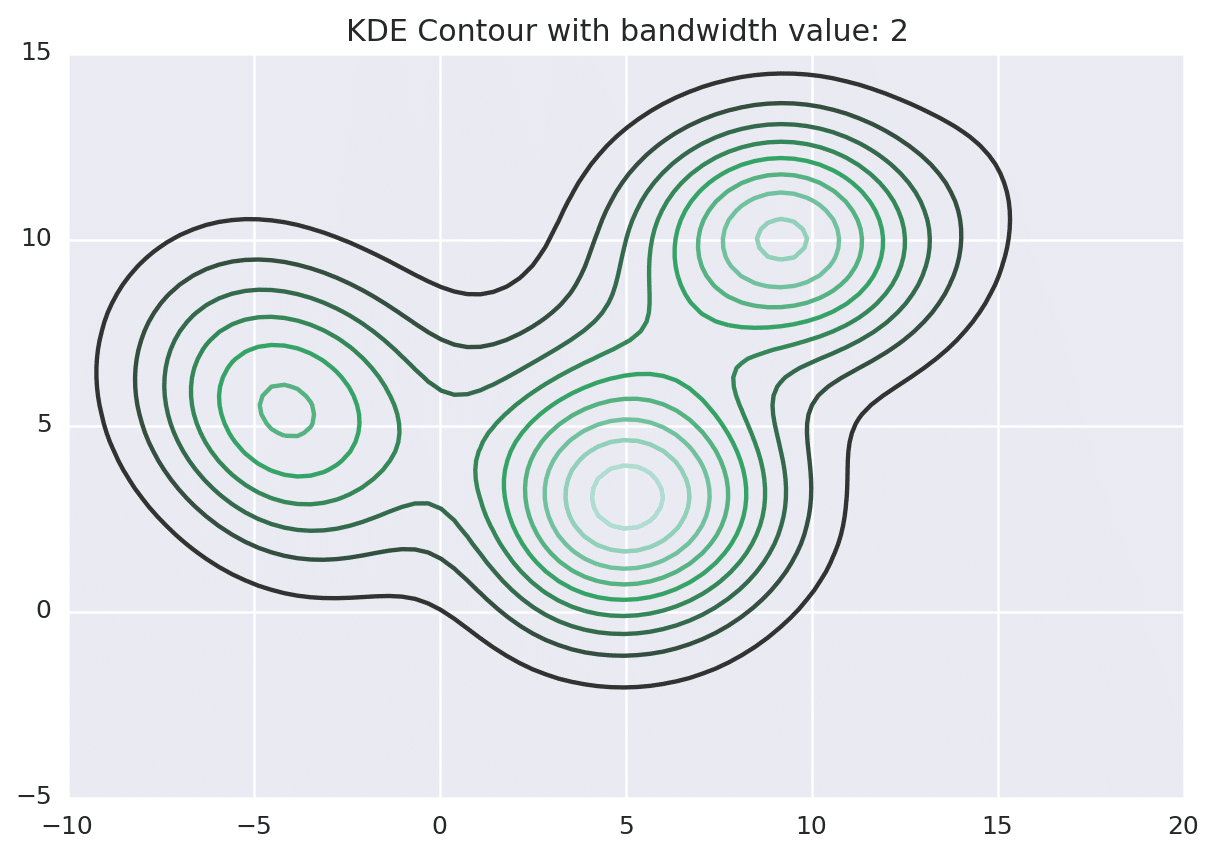
Below is the KDE surface for our points above using a Gaussian kernel with a kernel bandwidth of 2. The first image is a surface plot, and the second image is a contour plot of the surface.
Mean Shift
So how does mean shift come into the picture? Mean shift exploits this KDE idea by imagining what the points would do if they all climbed up hill to the nearest peak on the KDE surface. It does so by iteratively shifting each point uphill until it reaches a peak.
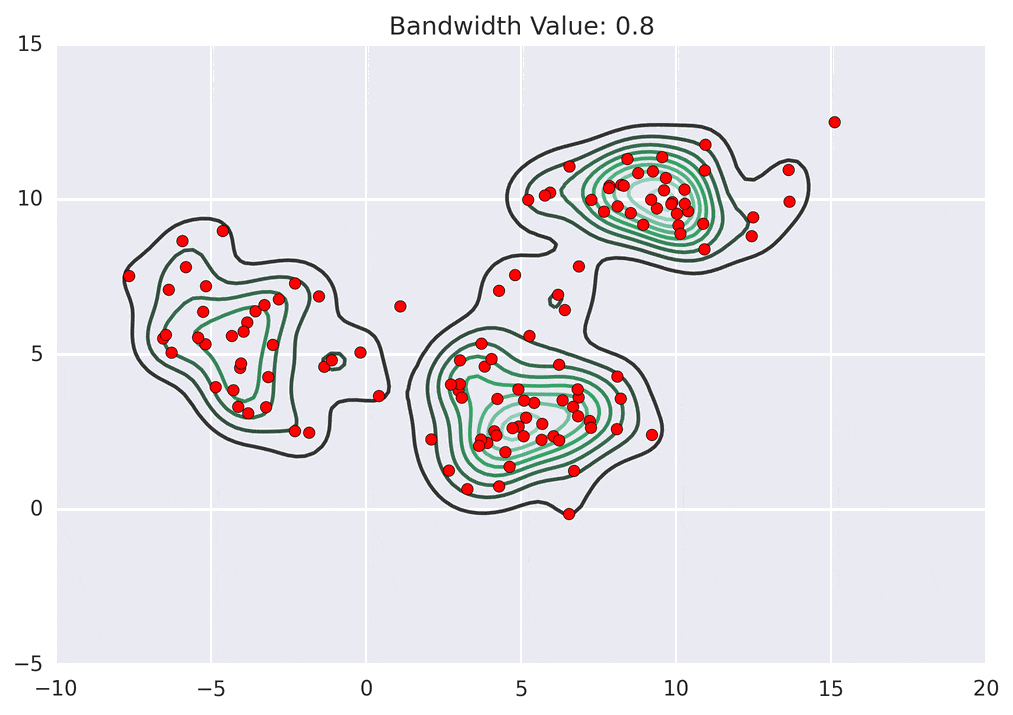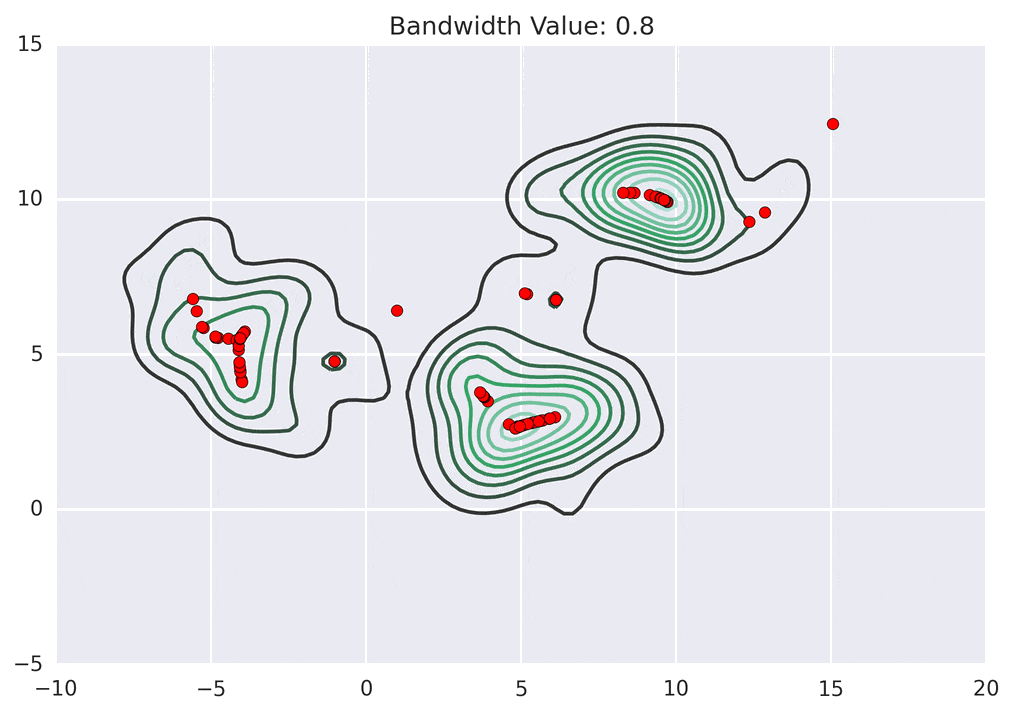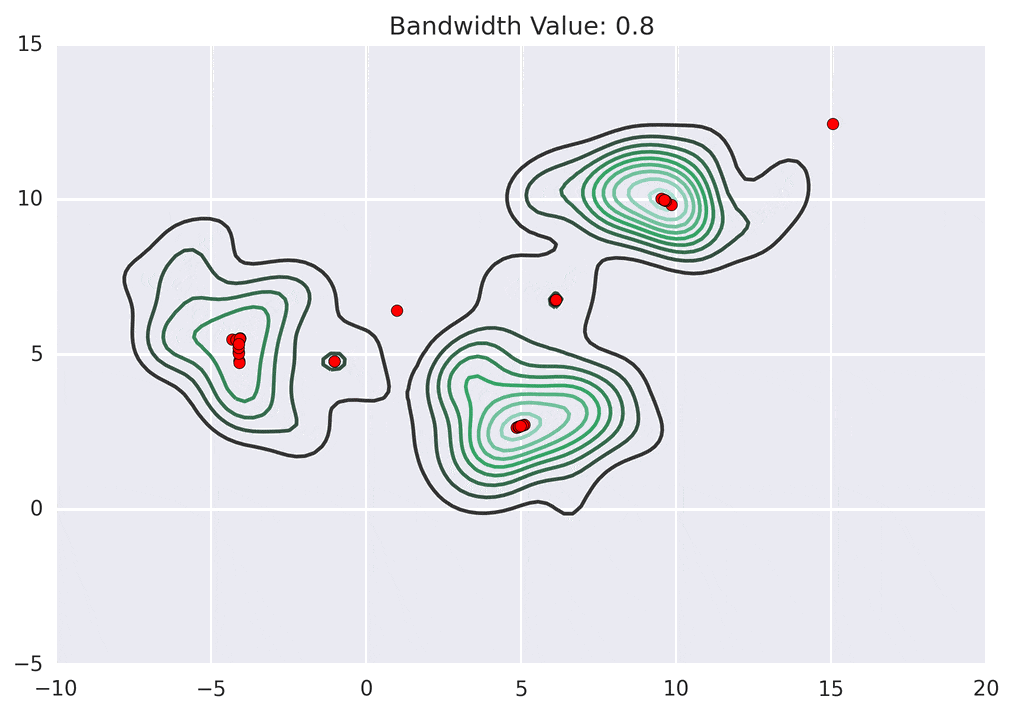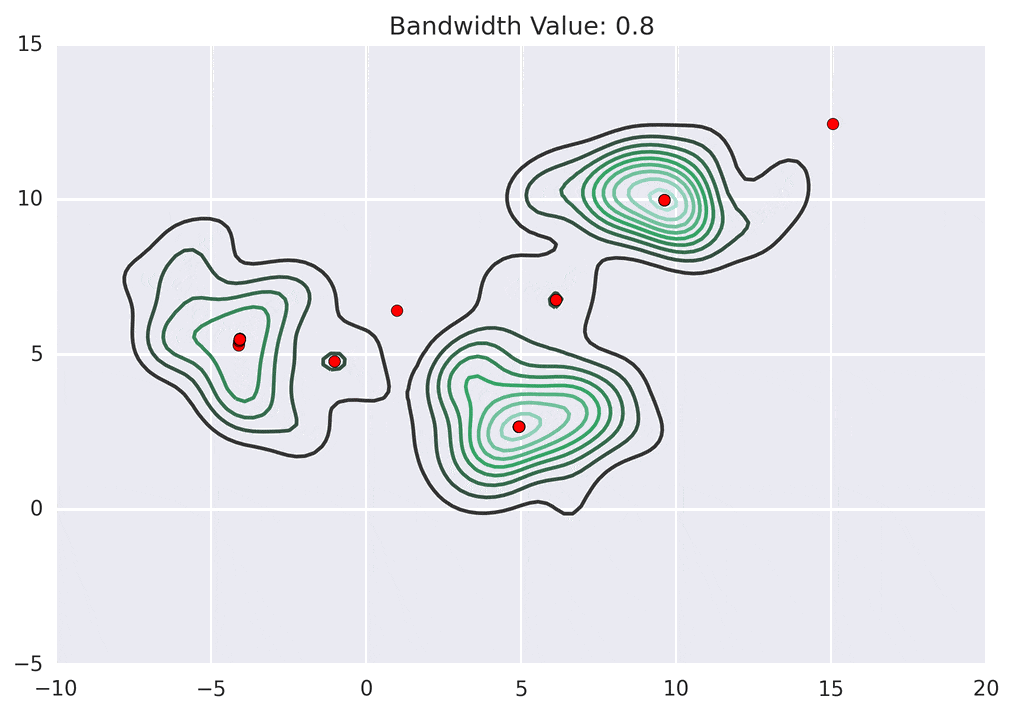
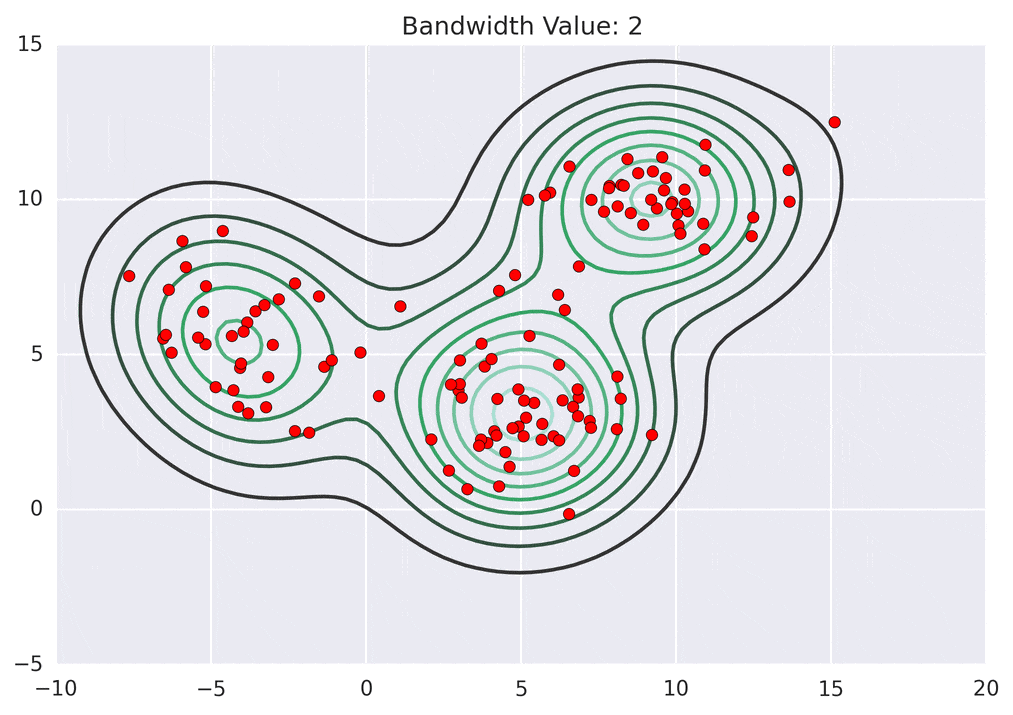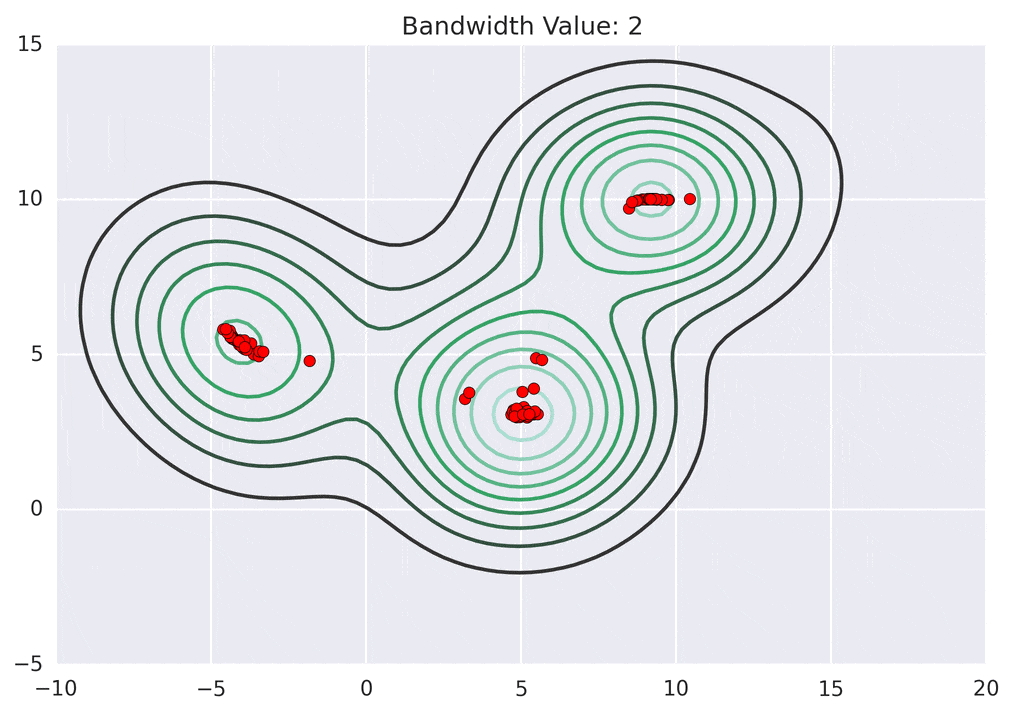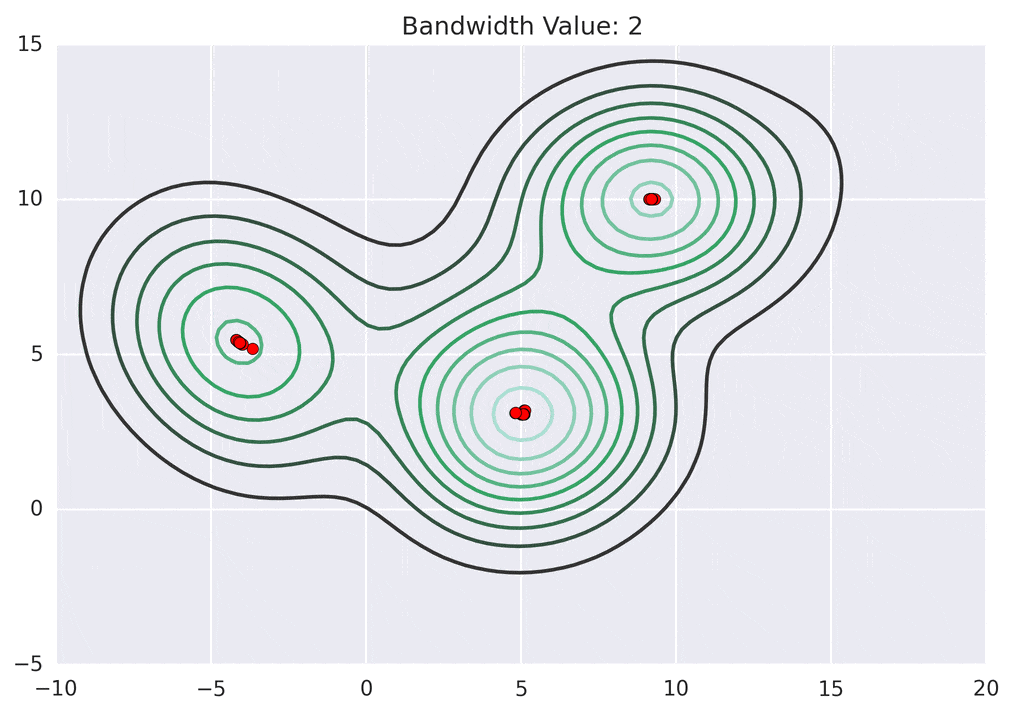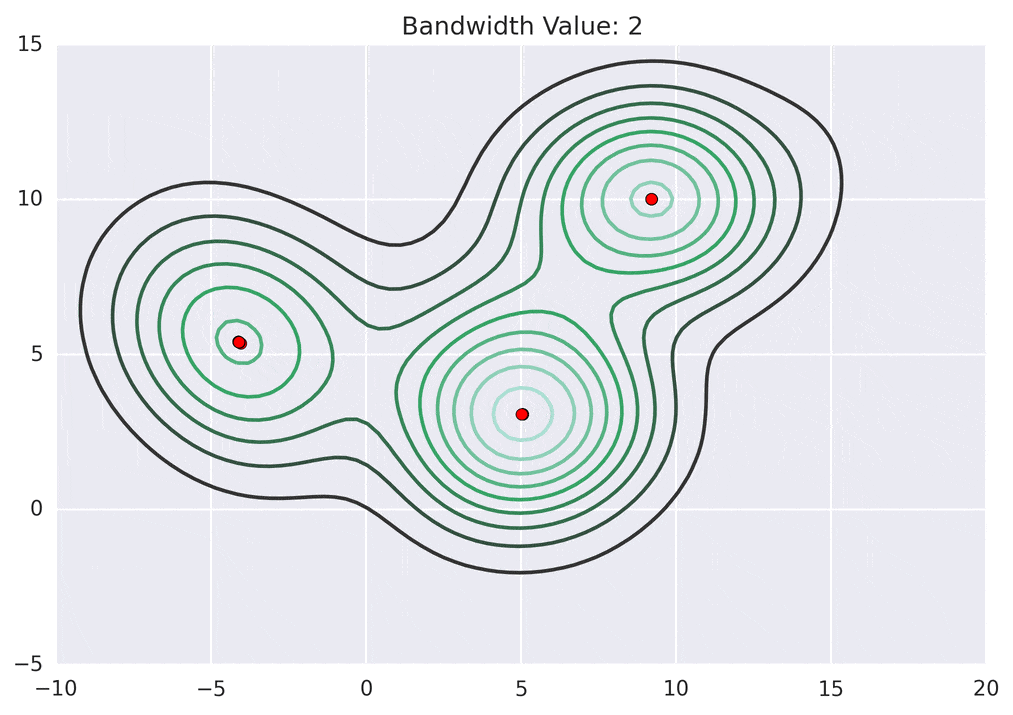
Depending on the kernel bandwidth used, the KDE surface (and end clustering) will be different. As an extreme case, imagine that we use extremely tall skinny kernels (e.g., a small kernel bandwidth). The resultant KDE surface will have a peak for each point. This will result in each point being placed into its own cluster. On the other hand, imagine that we use an extremely short fat kernels (e.g., a large kernel bandwidth). This will result in a wide smooth KDE surface with one peak that all of the points will climb up to, resulting in one cluster. Kernels in between these two extremes will result in nicer clusterings. Below are two animations of mean shift running for different kernel bandwidth values.
The top animation results in three KDE surface peaks, and thus three clusters. The second animation uses a smaller kernel bandwidth, and results in more than three clusters. As with all clustering problems, there is no correct clustering. Rather, correct is usually defined by what seems reasonable given the problem domain and application. Mean shift provides one nice knob (the kernel bandwidth parameter) that can easily be tuned appropriately for different applications.
The Mean Shift Algorithm
As described previously, the mean shift algorithm iteratively shifts each point in the data set until it the top of its nearest KDE surface peak. The algorithm starts by making a copy of the original data set and freezing the original points. The copied points are shifted against the original frozen points.
The general algorithm outline is:
for p in copied_points:
while not at_kde_peak:
p = shift(p, original_points)
The shift function looks like this:
def shift(p, original_points):
shift_x = float(0)
shift_y = float(0)
scale_factor = float(0)
for p_temp in original_points:
# numerator
dist = euclidean_dist(p, p_temp)
weight = kernel(dist, kernel_bandwidth)
shift_x += p_temp[0] * weight
shift_y += p_temp[1] * weight
# denominator
scale_factor += weight
shift_x = shift_x / scale_factor
shift_y = shift_y / scale_factor
return [shift_x, shift_y]
The shift function is called iteratively for each point, until the point it not shifted by much distance any longer. Each iteration, the point will move more closer to the nearest KDE surface peak.
Image Segmentation Application
A nice visual application of mean shift is image segmentation. The general goal of image segmentation is to partition an image into semantically meaningful regions. This can be accomplished by clustering the pixels in the image. Consider the following photo that I took recently (largely because the nice color variation makes it a nice example image for image segmentation).
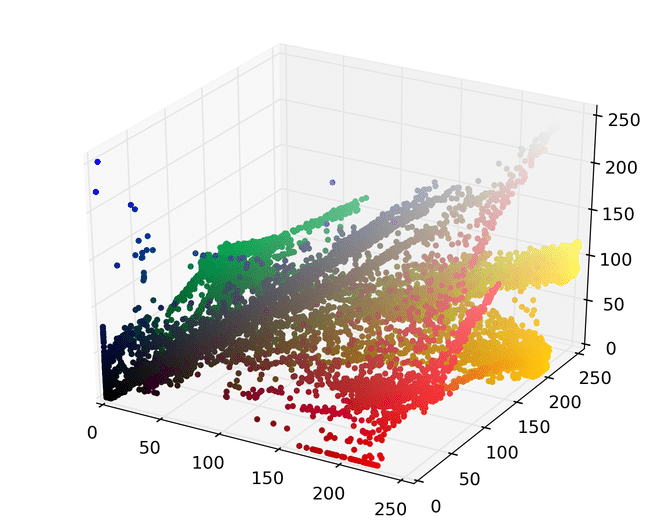
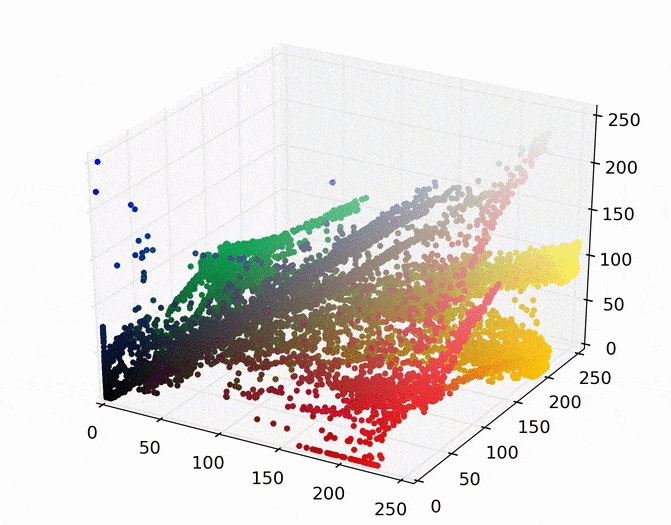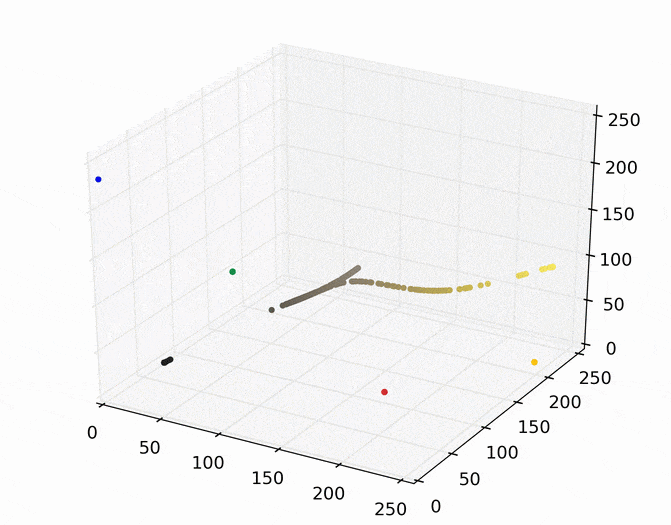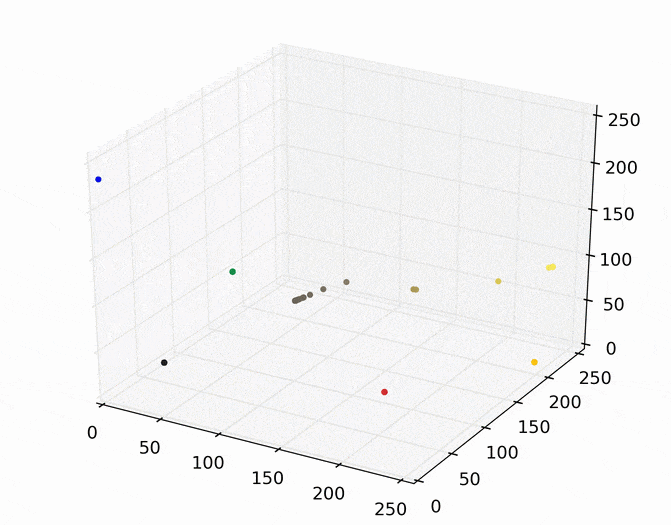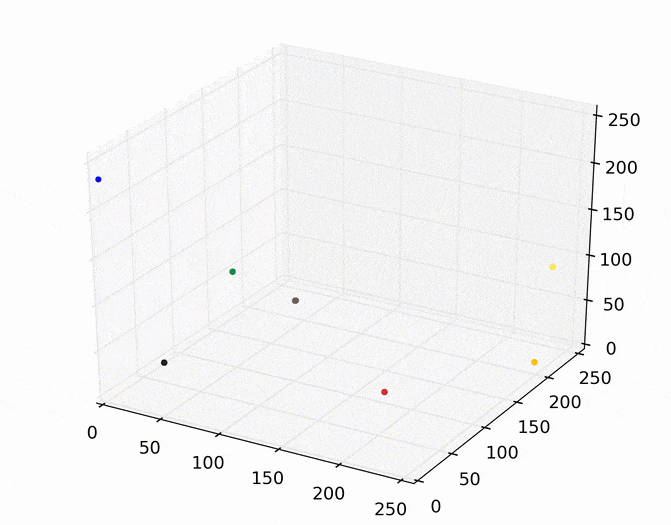
The first step is to represent this image as points in a space. There are several ways to do this, but one easy way is to map each pixel to a point in a three dimensional RGB space using its red, green, and blue pixel values. Doing so for the image above results in the following set of points.
We can then run mean shift on the above points. The following animation shows how each point shifts as the algorithm runs, using a Gaussian kernel with a kernel bandwidth value of 25. Note that I clustered scaled down version of the image (160×120) to allow it run in a reasonable amount of time.
Each point (e.g., pixel) eventually shifted to one of seven modes (e.g., KDE surface peaks). Showing the image using the color of these seven modes produces the following.
Comparison to Other Approaches
As I mentioned above, I really like mean shift because of its simplicity. The entire end result is controlled by one parameter—the kernel bandwidth value. Other clustering approaches, such as k-means, require a number of clusters to be specified as an input. This is acceptable for certain scenarios, but most of the time the number of clusters is not known.
Mean shift cleverly exploits the density of the points in an attempt to generate a reasonable number of clusters. The kernel bandwidth value can often times be chosen based on some domain-specific knowledge. For example, in the above image segmentation example, the bandwidth value can be viewed as how close colors need to be in the RGB color space to be considered related to each other.
Mean shift, however, does come with some disadvantages. The most glaring disadvantage is its slowness. More specifically, it is an N squared algorithm. For problems with many points, it can take a long time to execute. The one silver lining is that, while it is slow, it is also embarrassingly parallelizable, as each point could be shifted in parallel with every other point.



Thanks for the well written post, very useful.
I’m curious about the preference over using a kernel bandwidth over using a specified number of clusters. While it is true that you won’t know the number of clusters before hand, you also don’t know the bandwidth to use, and so you are essentially leaving the number of clusters up to luck – you could just generate random numbers?
I intuitively like the approach better too, but am curious as to your take on the distinction.
Thanks for the comment. Unfortunately, there is no easy answer to your question, it really depends on the situation.
There are situations where you know the number of clusters a priori. For those, using a clustering approach where the number of clusters is specified makes the most sense.
When you don’t know the number of clusters up front, you need some method to compare different clusterings (to determine which one is the best). There are several ways to do this – ranging from qualitative inspection (e.g., just looking at the results and choosing the one that looks the most reasonable), to various cluster scoring metrics [1]. If you have an idea of how “close” observations need to be to be similar mean shift can work really well, as the kernel bandwidth represents this “neighborhood distance”.
With respect to k-means specifically, mean shift has some nice advantages. A significant limitation of k-means is that it can only find spherical clusters. Mean shift uses density to discover clusters, so each cluster can be any shape (e.g., even concave). On the other hand, k-means is significantly faster than mean shift.
[1] http://en.wikipedia.org/wiki/Determining_the_number_of_clusters_in_a_data_set
Thanks for your reply. I hadn’t really appreciated the fact that K-Means has the spherical limitation. Also, it occurs to me that choosing a bandwidth lets you see how the clusters change continuously against the bandwidth, rather than just trying a few random numbers.
Interesting stuff either way!
Very good article to make it easy to understand what mean shift is and how it can be used.
Thank you for the post. It helped me a lot understand the mean shift algorithm.
I would like to make the same animations as you did in the post (those that the points result at the KDE peaks for different kernel bandwidth values). Which dependencies have you used? It would be helpful if you could upload some sample code for these animations.
Thanks in advance.
Hi John, I used Matplotlib to generate the plots and Seaborn to add some nicer styling to them. The central idea is to create a plot for each iteration of the algorithm, and save it as an image. Then, take the sequence of images and turn them into an animation.
The code I have on github has this method in mean_shift.py
def cluster(self, points, kernel_bandwidth, iteration_callback = None)If you pass in an iteration_callback function, the mean shift code will call it after each iteration with the current state of the algorithm. You can plot the state inside of the callback.thank u so much.great written post
Thank you so much for writing this post. The visualizations and clear examples really worked to cement some of the concepts I’ve been reading through in the peer-reviewed literature. Hopefully journals start to update their requirements along these lines for methods papers. Also very thankful for the pytjon code provided, it allows me to play around with my own data.
Thanks Nick, I’m glad you found it helpful and I appreciate the nice words.
Dear Matt, thank you for this very practical and useful post related to Mean Shift Clustering. It has been quite difficult to encounter intelligible material about this algorithm. I converted your code in Python to Matlab and added KNN to adapt the bandwidth for each point (Adaptive Mean Shift). I have a question related to the first and second figures (KDE surface and contour plot of this surface, respectively). How did you generate these figures with Matplotlib? In Matlab, I used surf() and contour() function, but the result seems to be not correct (maybe I have forgotten something regarding to points [-10:20,-10:20] on Gaussian kernel with bandwidth = 2). Have you established any mean vector and covariance matrix from the points in each cluster (after mean shift process with bandwidth = 2)?
Hi Adam, thanks for the comment.
I used matplotlib’s
plot_surfaceto generate the blue KDE surface plots.For the contour plot, I used Seaborn:
http://stanford.edu/~mwaskom/software/seaborn/generated/seaborn.kdeplot.html
I haven’t used Matlab in a while, so I’m not sure what the Matlab equivalents would be. In general though, your approach of discretizing the space into a 2D grid, applying the KDE function over each grid cell, and plotting that as a surface has been how I’ve always done it.
Adam, do you have this Matlab code available anywhere? I’m interested in trying Adaptive Mean Shift but haven’t been able to find code in a language I understand.
Hi Matt, great article by the way. It helped me a lot.
I am trying to generate like you did, the KDE surface plots and the contour plots of a dataset on which later I am going to apply your mean shift algorithm. I want to do that in order to have an idea of the expected number of clusters that mean shift will generate. If I am not mistaken, your version of the algorithm uses a gaussian kernel. So, I want to apply via scipy’s gaussian_kde the same bandwidth value for a gaussian kernel on the dataset and with matplotlib’s plot_surface and seaborn’s kdeplot to generate the KDE surface plot and contour plots respectively. My problem is that although the contour plots seem to generate similar results to the mean shift algorithm, the gaussian_kde does not. For bandwidth values larger than 1 or 2, I get a huge cone for the whole dataset. Did you use scipy’s gaussian_kde as well?
Hi Matt, I am trying to generate the KDE surface plots and contour plots as you did. Since, your version of the mean shift algorithm is based on a gaussian kernel, I am trying to get an indincation of the number of the clusters the algorithm yields for each bandwidth value, by applying the same bandwidth value to scipy’s gaussian_kde and seaborn’s kdeplot. Although, seaborn seems to generate a contour plot that seems to be in agreement with the number of clusters the mean shift algorithm generates, scipy’s gaussian_kde does not. For bandwidth values larger than one, I get surface plots looking like a cone for the whole dataset, which theoritically would lead to one cluster. But, the mean shift algorithm generates different number of clusters.
I am using scipy’s gaussian_kde for the kernel density estimation and matplotlib’s surface_plot in order to plot is as surface. Have you also used the same functions for these plots? Do you have an idea what might be going wrong?
Thanks in advance.
Hi John,
I’ve never used the scipy gaussian_kde function. I just skimmed through the docs for it (http://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.gaussian_kde.html). It says that the bandwidth is determined automatically unless you provide a scalar value. I imagine you are providing a scalar. It’s not clear to me though, if the scalar is used directly as the bandwidth, or if it’s used as an input to another function. I tried finding where it’s used in the source code (https://github.com/scipy/scipy/blob/v0.17.1/scipy/stats/kde.py#L41-L537), but couldn’t quickly find it. I may take another look later if I have some time.
Another thought I had is that although “gaussian” has a concrete meaning, people often approximate a gaussian function by using different constants and such. It’s possible the “gaussian” calculation could be slightly different between different implementations.
Hope this helps.
Yes, I provide a scalar value. With the same value I feed the mean shift algorithm as well. Mmm, I see. What procedure did you follow for the generation of the KDE surface plot? My data is 2D, as yours.
Hi Matt,
According to what I understood KDEs are estimated probability distribution functions based on an assumed underlying distribution like guassian or epanechnikov distributions, is that right?
The function ‘kernel’ in your code, is it the KDE. If it is then shouldn’t x and y coordinates be the arguments of the function, if not is the underlying kernel distribution – in that case why give bandwidth as argument , isn’t bandwidth an argument to KDE but not the underlying assumed distribution.
Hi Dhanush,
In this example the KDE concept is used to conceptualize a probability function that could have generated the data that we have.
In other words, we start with some data (2D points). You can imagine that if we randomly sampled some probability distribution, we may have ended up with those points. What would such a probability function look like? Constructing a KDE helps us to answer this question. The KDE is constructed by placing a kernel (weighting function, or conceptually a little hill or bump) on each point. Adding all of those kernels up gives us the overall KDE function.
Depending on the size of the kernel (defined by the bandwidth value), the shape of the overall KDE surface will vary. The points could have been sampled from any one of these surfaces with similar likelihood (there is no “one” surface that could have generated the points better than another).
Mean shift works by exploiting this KDE concept, and marching each point up to the nearest peak on the KDE surface. We don’t actually know what the formula for the KDE surface is, but since we’re constructing it using the points we are able to evaluate it at any given (x,y) location.
Does this help?
Hi Matt,
I tried to make function of mean shift clustering on C#. But I did not find any hint(source code of C, C++) yet. If you don’t mind, can you help to me??
Hi Matt, I’m new to python and mean shift clustering. Thank you for your post, this was very helpful especially to a non-technical like me. I may have a basic question here, hope you can help. I ran your code and saw that your data.csv (125×2) file neatly forms into 3 clusters. My question is, what if my data has three or more dimensions (i.e. 125X3) like in your RGB example? How do I set up the data? and will your mean_shift.py work?
Hi Carla,
My implementation should work for data of any dimension. Instead of having 1×2 vectors (2D points, or 1×3 vectors (3D points), you’ll just pass in an array 1xN vectors (i.e, an array of 1xN arrays) where N is the dimensionality of your data. Have you tried running it with higher dimensional data?
– Matt
Hi Matt, I also read your post, your post is helpful for me. As you know, in mean shift clustering, window-size is very important. If this value is small, computational time is very long, and this value is big, the quality of clustering is low. Can I ask to you your good comment about window-size??
Hi Matt,
Thanks for the blog! It is wonderfully written :)
I understand that the bandwidth value for the kernel is the most important parameter that decides the cluster means.
You have said that the Gaussian kernel is the most commonly used one. But does the type of kernel we use influence the output? If we know that our clusters have a specific shape in space, then would it make sense to use a kernel function that approximates that shape?
Hi Kaaviya,
The type of kernel used can certainly influence the output.
However, Gaussian kernels should allow most shapes to be recognized in clustering results. One of the nice aspects of Mean Shift is that it is able to cluster arbitrary (e.g., non spherical) shapes.
I don’t think it necessarily makes sense to use specialized kernel shapes in most situations. The kernel defines the shape of importance around each point. Gaussian kernels allow you to give equal importance in every direction from a given point, but as you get further away from the point the importance decays in an gaussian way.
The importance doesn’t have to decay in a gaussian manner though. For example, you could use a flat (also called uniform) kernel, which usually defines a circular (or spherical) region around each point, and gives equal weight to all points within the region, and zero weight to points outside. Alternatively, you could use a linear kernel that allows the weight to decay in a linear manner as you get further away from each point. Often times these kernels are used to improve performance, as you can ignore points that fall outside of the kernel during each iteration of the algorithm (if you can figure out what point those are efficiently).
See the “Kernel Functions in Common Use” section – https://en.wikipedia.org/wiki/Kernel_(statistics)
The goal of the kernel is to help understand the probability function that may have generated the data. I have seen adaptive kernel approaches that vary the kernel bandwidth depending on the density of points in a local area, in an attempt to better estimate the underlying probability function.
Hi Matt,
Thanks for the reply!
I am trying to extract ellipsoidal objects from lidar data and I have some promising first results from mean-shift. I am using Gaussian kernel with band-widhts X = Y << Z which looks for clusters within a cylinder.
Your answer helped me understand better what I am doing. And I feel that Gaussian kernel is a better choice compared to the ones available.
Have a nice day!
Hi Matt,
Thanks for your information.
As I understood, mean shift algorithm needs input value of band width like K value in k-means algorithm.
If input K value is disadvantage in k-means then input band width is also one of the disadvantage. If so, how to overcome this?
And also, how to overcome is its slowness? Because slowness of any algorithm is main disadvantage. With this slowness how to consider this algorithm rather than k-means, Fuzzy c-means algorithms.?
Hi, Matt, thank you so much for your post. It helped me a lot to understand Mean Shift.
By the way, I created MeanShift_js nodejs module based on your work. Here is the link: https://github.com/sunzhuoshi/MeanShift_js
I added your name into the license file(MIT), thanks again!