Article summary
In graph theory, traversal of graphs is done for a variety of reasons. Generally, the vertices are the information we care about, and the edges just show the relation between the vertices.
In some problems, though, the edges are what’s important. Problems like this can be common for maps where the edges represent roads and the vertices are where roads intersect. So how can we transform our graph for edge traversal?
A Problem to Consider
Let’s say we want to walk the neighborhood in a circuit and only walk each street once. It should be clear that every vertex needs to be of even degree or, to put it another way, that every intersection needs to connect an even number of streets. (If you have a cul-de-sac, a circuit can’t be formed, unless you wanted to walk every street in both directions.)
So our neighborhood looks like this, with my house located at D:
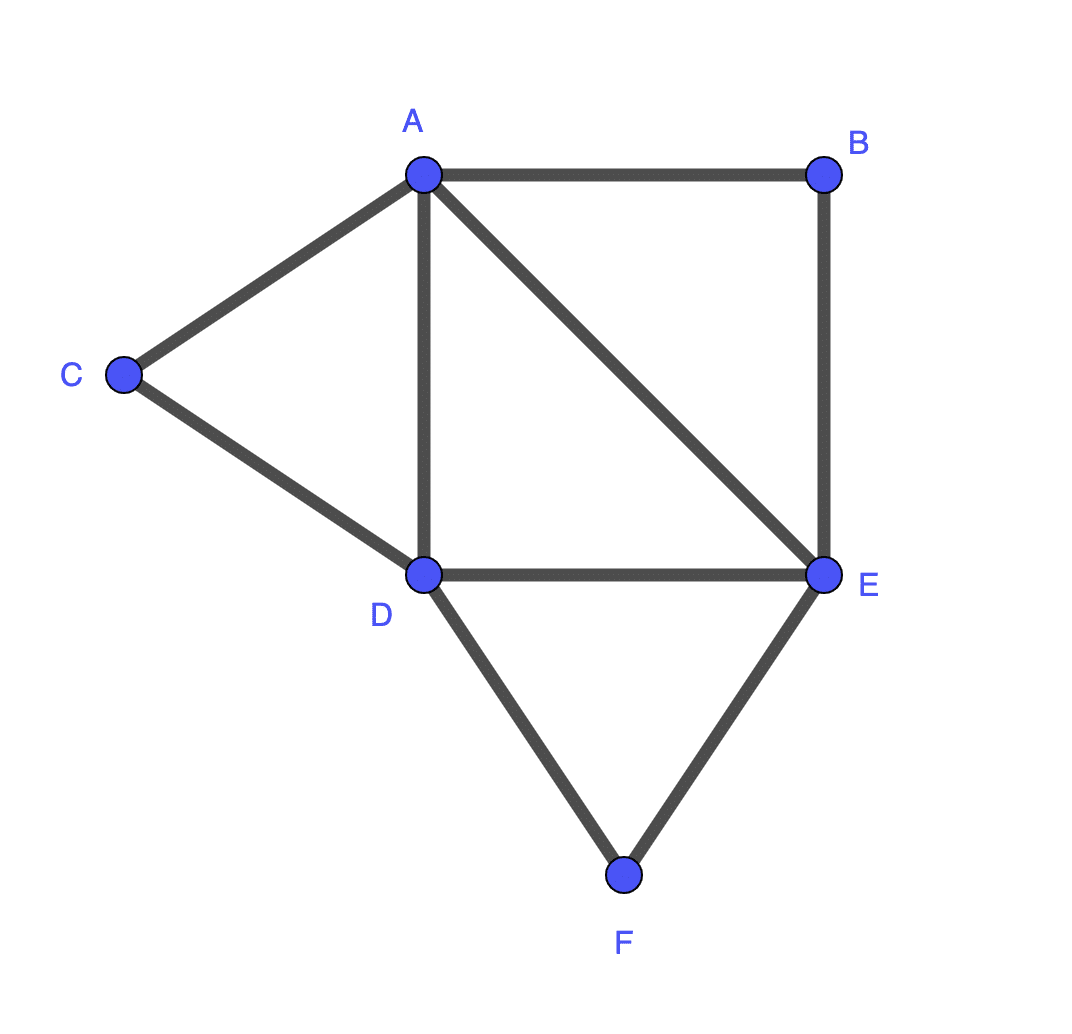
Visually, we can find a path: D > A > B > E > A > C > D > E > F > D
We aren’t trying to hit each intersection at most once, and we aren’t finding the Hamiltonian Path, so this works out. We can also notice that we will hit each intersection n/2 times, where n is the number of streets connected to that intersection (except the starting intersection, which will be n/2+1 because it’s a circuit).
Why Transform the Graph?
It’s entirely possible to solve this problem without any changes; this is finding the Eulerian Cycle.
However, we could change this graph to have the edges represented with vertices, then connect those new vertices by edges if they shared a vertex in the original graph. This is known as the Line Graph or edge-to-vertex dual graph.
For this example problem, it might not seem all that useful, but knowing how to transform one problem into another is incredibly useful. It can give us a different way of understanding the original problem, helping us find the solution. Say you needed to find some edge coloring of a graph. You could convert the graph into its line graph and solve for graph/vertex coloring, which would give you the correct result.
The Line Graph
This is what the line graph of our problem looks like, where the vertices are now labeled with the vertices connected to the edge in the original graph. Each vertex is connected to all others that share a letter.:
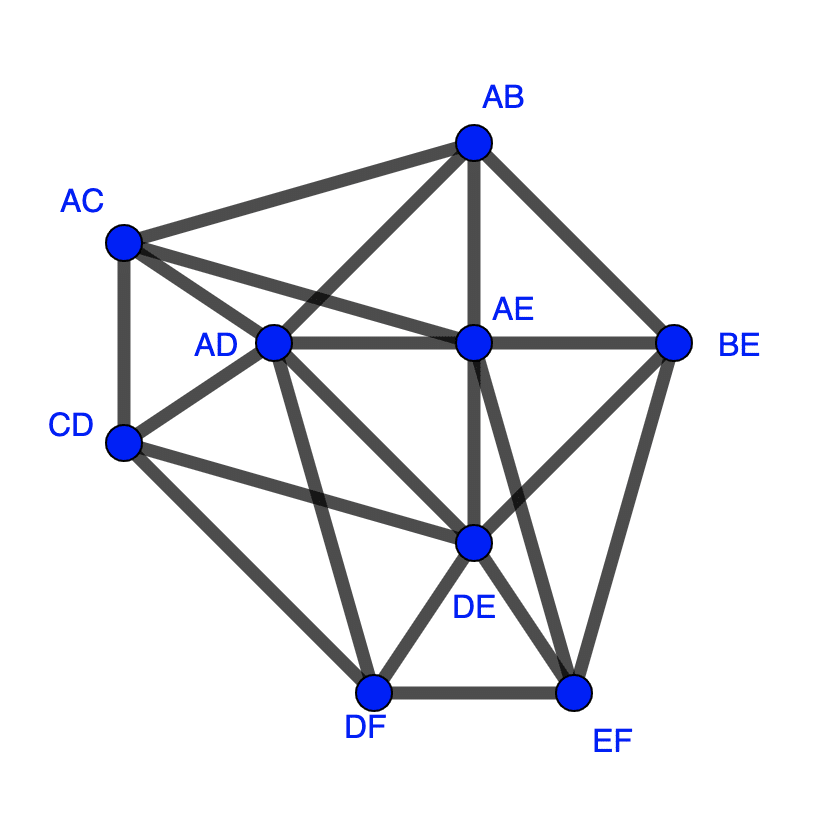
With this, we can now solve for the Hamiltonian cycle — but with one caveat. Certain routes from our current vertex we can’t take based on the previous vertex, or rather the direction we took along the edge in the original graph. For example, in the original solution above, we took edge AD and then AB. With this line graph, it looks like we could then go to AC, but in the original graph, this is akin to backtracking and walking an edge more than once. This is because going from AD to AB means we must have traveled from D to A to B; this matches the original solution.
What can we do here to make our possible decisions easier to see? Order the letters in the labels to denote the direction of travel in the original graph. So AD becomes DA, then AB is fine since we are starting from A. That’s to say the first letter in the label is where we are starting from and the second is where we are ending. If we are in AB now then we can’t go to AC because it doesn’t contain B, which is where we need to start. So solving for the Hamiltonian cycle in this case we can use the order of the letters in the labels to determine where we can go, never changing the order once a vertex is visited.
From AB, we can only go to BE and then a choice of EA(AE), ED(DE), or EF, original label in parentheses. We can continue in this manner, backtracking if we get in a dead state, and get the original solution.
DA(AD) > AB > BE > EA(AE) > AC > CD > DE > EF > FD(FD)
I’ve provided one example, but line graphs can have many uses or allow you to see your problem in a new light. Viewing relationships or networks in another manner, in some cases, might be an easier way to solve the problem.
