The crossing numbers of graphs is an interesting topic in discrete geometry, graph theory, graph drawing, and computer science. Though simple at its core, it lends itself to ideas that are much more complex.
What Is a Graph?
Usually when someone talks about graphs in mathematics and computer science, they are referring to something like this:
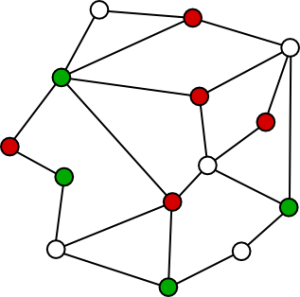
What we have are vertices (also called nodes), shown as the colored dots in these images, connected by edges, shown as the lines in these images. There can be any number of vertices which may or may not be connected by edges. If every vertex is connected to all other vertices, then it’s considered a complete graph.

A bipartite graph is one in which each vertex belongs in one of two sets, and vertices of the same set are not connected by an edge. This is usually shown by coloring the vertices, i.e. red and blue, where red vertices can’t be connected to other red vertices.
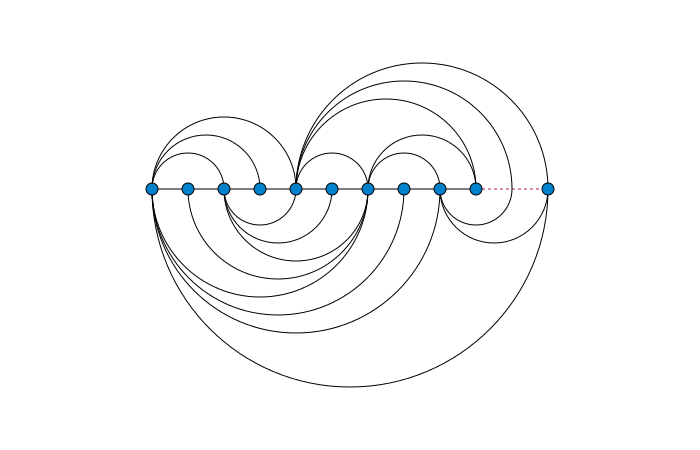
Depending on how the edges and points are drawn, you can create various types of graphs. Some examples include on the plane with straight edges (rectilinear), a graph containing no cycles (tree), all vertices on a line with curved edges (book embedding), or in some other space.

One important thing to note is that moving the vertices of a graph only changes the appearance of the graph, but it’s still the same graph.
What Are Crossing Numbers?
When a graph has a pair of edges that cross, it’s known as a crossing on the graph. Counting up all such crossings gives you the total number for that drawing of the graph. Therefore, one of the main problems is to minimize the number of crossings by adjusting the positions of the vertices.
This is usually done to improve the readability of graphs or to solve some real-world application such as VLSI and circuit board design or road or railroad crossings. The minimum number of crossings in any drawing of a graph is known as the crossing number.
Computing the crossing number is an NP-hard problem, which means there is no algorithm that can find the minimum number of crossings of any graph in deterministic polynomial time. For rectilinear complete graphs, we know the crossing number for graphs up to 27 vertices, the rectilinear crossing number.
Since this problem is NP-hard, it would be at least as hard to have software minimize or draw the graph with the minimum crossing, except for graphs where we already know the crossing number. In all other cases, it is best to have a triangular convex hull. You can discover why by manually drawing complete graphs with a low number of vertices.
What Is a Local Crossing Number?
Though there is a lot of study around the crossing number, one area that has received less attention is the local crossing number. The local crossing number of a drawing of a graph is the largest number of crossings on a single edge. The minimum local crossing in any drawing of a graph is the local crossing number for that graph. This is a concept I’ve researched with two professors and other students, a shameless plug.
Both are interesting areas of research and can have lots of applications. Graph drawing in general can lead to some interesting visualizations and even art.
Though the construction of proofs can be difficult or the problems complex to solve, it’s a fun area to explore due to the hidden complexity and interactive, visual qualities.
If you’re curious about this subject, more in-depth information on crossing number variants can be found in The Graph Crossing Number and its Variants: A Survey.