Article summary
The narrator of Edwin Abbott’s classic Victorian satire Flatland is a commoner, a simple, two-dimensional square. He lives in a two-dimensional world filled with other flat characters: line segments, triangles, higher-sided polygons, and circles.
Circles, in Flatland, constitute the upper classes of society, but if Abbott’s humble narrator had been born in a different flatland, he could have been a square and a circle.
Impossible, you say? Allow me to introduce you to TaxicabLand.
Like Flatland, TaxicabLand is a two-dimensional world, but there is something distinctly different about it. If you ask Mr. Square-Circle how far it is from his front door to the corner of his property, he will not measure the distance in a straight line. Rather than measuring the shortest distance, he first measures the distance north or south, then the distance east or west, then adds the two numbers together. Rather than using Euclidean geometry like Flatland does, it uses a different geometric system known as taxicab geometry.
That is the essence of TaxicabLand. All distances are measured not as the shortest distance between two points, but as a taxi driver might count the distance between Point A and Point B: so many blocks one way plus so many blocks the other way.
And that one small change has profound effects.
Circles
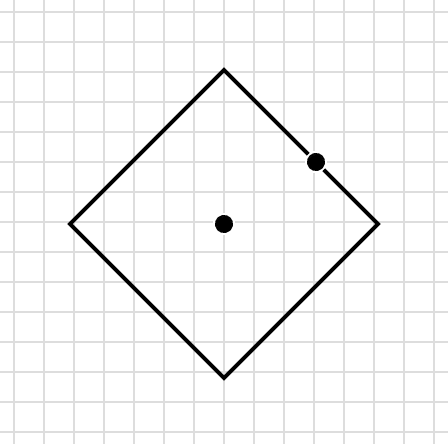
The reason Mr. Square can also be Mr. Circle in TaxicabLand is because in his world, there’s nothing inherently contradictory about the definitions of a square and a circle. A square is a shape with four sides of equal length and four equal angles. A circle is all the points that are the same distance from a particular point, what we usually call the circle’s center. Since the definition of a circle depends on distance, the shape of a circle changes when we change the definition of distance. Here’s how a circle looks in TaxicabLand.
Each point on the circle is the same distance from the center, but you’d be hard pressed to draw this circle with a compass. You’d be better off using a straight-edge.
If Mr. Square-Circle wants to live exactly five miles from work, he must look for a house somewhere on the edge of this diamond-shaped circle.
Ellipses
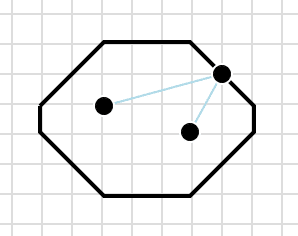
Ellipses, too, are defined in terms of distance. Mr. Square-Circle and his wife want to know where they can live so that when they drive to their respective workplaces in the morning, they only put eight total miles on their two cars. It doesn’t matter which car goes farther; they’ll switch the next day to keep wear and tear even. What are their options?
The workplaces of Mr. and Mrs. Square-Circle are the foci of this octagonal ellipse.
But even though circles and ellipses look very different than they do in plain old Flatland, they’re still cousins. If the two foci of a TaxicabLand ellipse are in the same place, the ellipse becomes a circle, just the way we’re used to—a small bit of comfort in an otherwise strange world.
Midsets
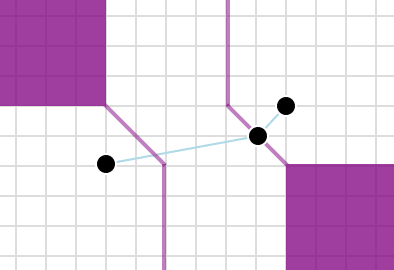
In Flatland, there is a phenomenon known as a “perpendicular bisector,” a line that cuts another line straight through the middle at a right angle to the first line. But a perpendicular bisector has another property: All its points are the same distance from each end of the line it cuts in two. The residents of TaxicabLand call this kind of line a “midset.” Midsets come in many shapes.
Some would look familiar to a Flatlander.
Most would not.
And some very special midsets make the leap from being a line to being an area.
After Mr. and Mrs. Square-Circle got married, they agreed to live the same distance from each of their parents. They studied the midset of the line connecting their parents’ two houses to know where they should go house hunting.
Parabolas
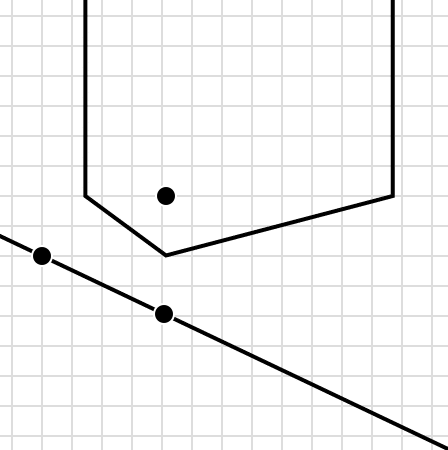
When Mr. Square-Circle was a young bachelor, he decided to live the same distance from his favorite hangout—the local library—and the highway that would take him into the big city. Here’s where he looked for apartments.
In Flatland, this irregular shape is much more symmetrical. We call it a parabola—the set of points the same distance from a line and another point. The parabolas of TaxicabLand bear some similarity to Flatland’s parabolas, but they’d be easy to miss if you didn’t know what you were looking for.
(Bonus question: When Mr. Square-Circle throws a ball, which parabolic arc does it follow—Flatland’s or TaxicabLand’s? Leave your answer in the comments.)
Hyperbolas
The last shape we’ll study today is the hyperbola.
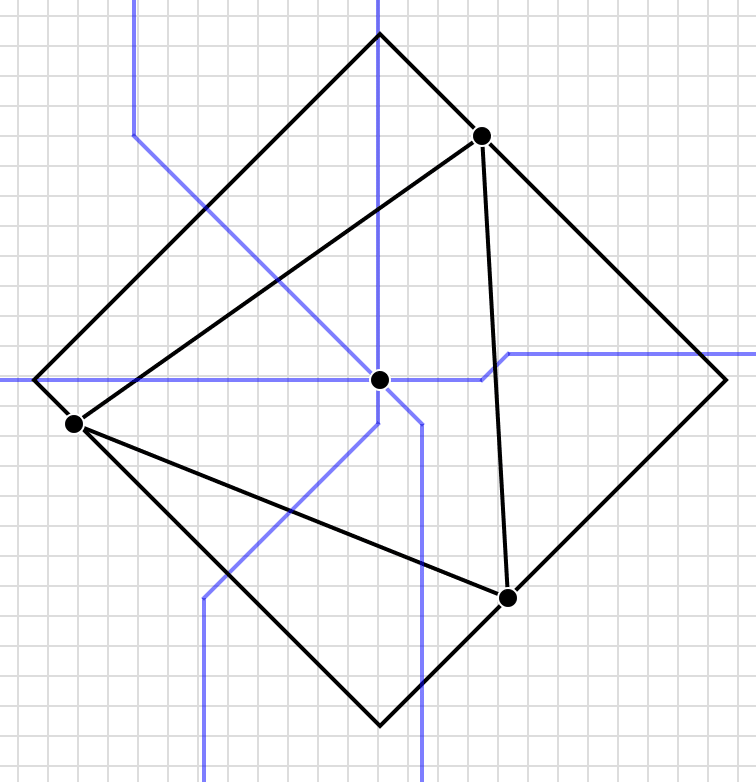
As the Square-Circle family grows, Mr. and Mrs. Square-Circle decide to take advantage of free, grandparental babysitting. They agree to live four miles closer to one set of grandparents or the other. Here are their options.
While these TaxicabLand hyperbolas may look like straight-edge versions of Flatland’s hyperbolas, their appearance can change. If the grandparents’ houses were in different places, the pair of acceptable hyperbolas would look more like midsets.
And as with midsets, if the grandparents in question live at certain addresses, the possibilities for Mr. and Mrs. Square-Circle open up dramatically.
Conclusion
You may have scratched your head when I said a square could also be a circle—you might even have jumped to disagree—but if you’ve had training as a mathematician, you knew what game I was playing. There’s nothing special about the math we learned in elementary school. It’s just like mathematical conclusions everywhere else: They depend on our assumptions.
The founders of TaxicabLand changed one assumption—how distance is measured—and many other things changed as a result: circles, ellipses, perpendiculars, even the angles between two lines. Changing one assumption changed their whole world.
So the next time you’re up against a contradiction—perhaps someone says you can’t increase both speed and quality—rather than just accepting their conclusion, you’ll take a look at the underlying assumptions. Just maybe you’ll find one that you can change, a single change that in turn changes the whole world.