Article summary
You may not be familiar with the concept of a control loop, but I guarantee that you use it in some capacity every day. A control loop is any system where a feedback mechanism is used to control a certain action.
When you catch a baseball traveling through the air, your eyes provide feedback which informs your brain where the ball is and how you need to move your hand in order to catch it. When you want to adjust the temperature of the shower before getting in, you feel the water with your hand, which provides feedback to your brain and determines whether you turn the knob to make the water hotter or cooler. These are examples of control loops.
Just as the human body uses feedback mechanisms and control loops, so do electronic and mechanical devices. A software algorithm called PID is often used to control these systems. PID is an acronym that stands for Proportional, Integral, and Derivative. Those of you who have taken calculus will recognize those terms but, to the rest of you, they might sound a bit intimidating. In this post, I will break down the three components of the PID algorithm and explain the purpose of each.
How PID Works
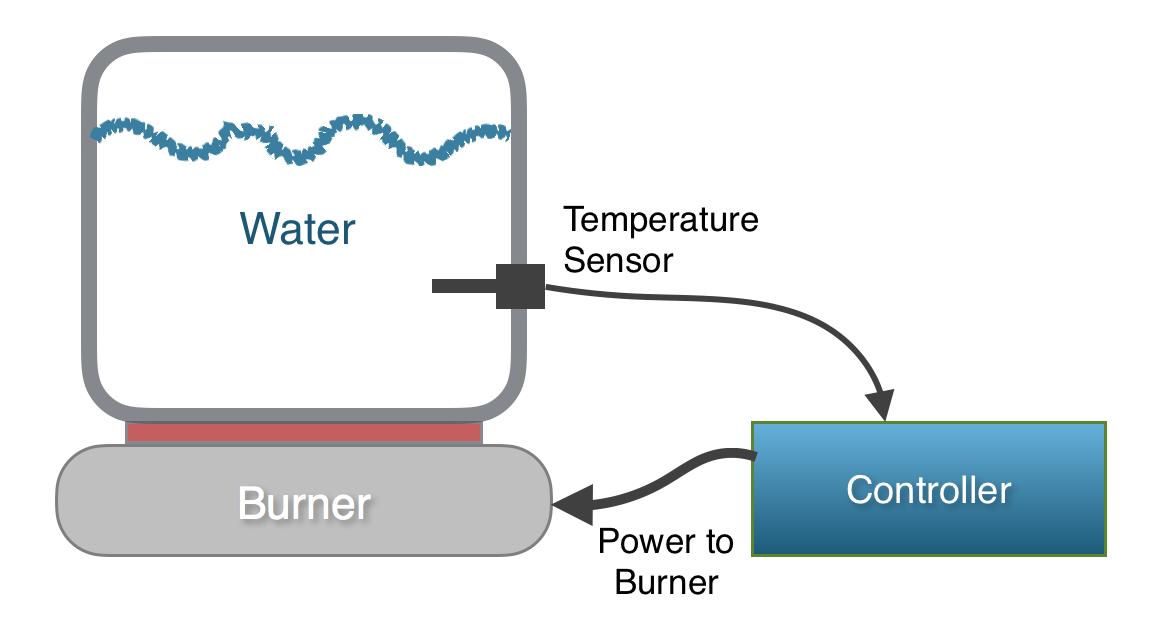
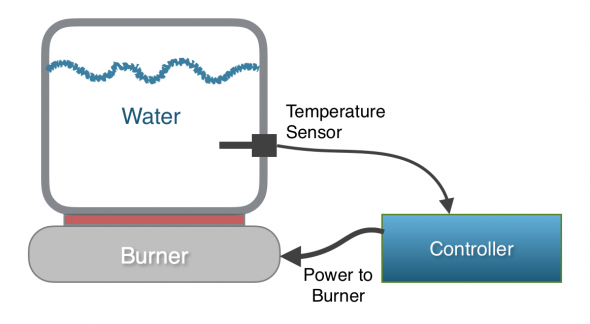
To describe how a PID algorithm works, I’ll use the simple example of a temperature controller. For this example, we have a system that includes an electric burner, a pot of water, a temperature sensor, and a controller.
The controller can read the temperature of the water using the temperature sensor, and it can adjust the power level of the burner from 0 to 100 percent. The software in the controller is responsible for adjusting the power level of the burner, such that the temperature of the water in the pot reaches a desired value (the set point) as quickly as possible and then maintains that temperature indefinitely. A PID algorithm could be used in the controller to solve this problem.
Proportional
The first component of the PID algorithm is the simplest to understand and the most crucial to the performance of the controller. The P stands for proportional. It means that the control variable should be adjusted proportionally to the amount of error in the system. A PID algorithm that only utilized a P component could be expressed as:
output = error * KpI just used a couple of terms that might sound unfamiliar, so let me explain.
Control Variable: The control variable is the output of the controller that we get to adjust. In our example, the control variable is the power level of the burner.
Process Variable: The process variable is the measured value in the system that you are attempting to control. The process variable is used as feedback to the controller so that it can decide how to adjust the control variable. In this case, it’s the process variable is the temperature of the water.
Error: The error is the difference between the process variable and the set point. In our example, the set point would be some temperature that we are trying to get the water to. The error at any point in time would be the difference between the current temperature and the target temperature.
The P component of the algorithm works by adjusting the output proportionally to the error. Let’s say the set point for the temperature controller is 100 degrees. If the measured temperature is currently 60 degrees, then the error is 40. The output of the controller would be set to 40 * Kp, where Kp is the proportional coefficient. Kp is a constant, non-negative value that is determined during the tuning process of the controller (we’ll talk more about tuning later). Now let’s say that the value of Kp is 10 (pulled out of thin air). Then the output of system would be (100 – 60) * 10 = 400.
You might be thinking, “400?! That’s way more than the 0 to 100% range of the burner. How can we set it to 400?” And you’re exactly right. This is called saturation, and it happens frequently in PID controllers. When saturation occurs, the control variable just needs to set the output to its maximum value, 100%. As the measured temperature approaches the target value, the error gets smaller and eventually the system becomes unsaturated. In our example, the system will become unsaturated at 90 degrees. At 95 degrees, the error would be 5 and the the output of the system would be 5 * 10 = 50%.
The problem with using a proportional-only controller is that it usually results in a steady-state error. As the error gets smaller and smaller, the result of the error multiplied by the proportional coefficient eventually becomes too small to have any affect on the process variable. This is because real-world systems are never 100% efficient. And that’s where the I component of the algorithm comes into play.
Integral
The I stands for integral, which is a mathematical term that means to accumulate something over time*. In the case of PIDs, the I component accumulates the error that occurs over time. That accumulated error is then multiplied by Ki, the integral coefficient, and added to the output. A controller algorithm that only utilized the P and I components could be expressed with the following pseudo-code:
accumulation_of_error += error * delta_time
output = (error * Kp) + (accumulation_of_error * Ki)The integral component of the control algorithm can remove any steady-state error in the system because it accumulates that error over time and compensates for it, rather than just looking at an instantaneous snapshot of the error at one moment in time.
Derivative
The D stands for derivative and is probably the most complicated. The derivative component is used less frequently in controllers but is still important in some applications. For the case of a pot of water sitting on a burner undisturbed, the D component is not necessary at all. However, if we complicate things by occasionally dumping handfulls of ice into the pot, then it could be helpful.
The derivative component is responsible for compensating for sudden changes in the error. If we dumped ice into our pot of water, the temperature would suddenly drop, the error would suddenly increase, and the derivative component of the algorithm would kick in and increase the output of the burner.
A derivative is a mathematical term that means “the slope of a curve.” In this case, the curve is the plot of the error over time. If the error is steady-state, then the result of the D component is zero. A full PID algorithm could be expressed by the following pseudo-code:
accumulation_of_error += error * delta_time
derivative_of_error = (error - last_error) / delta_time
last_error = error
output = (error * Kp) + (accumulation_of_error * Ki) + (derivative_of_error * Kd)The derivative component is mostly useful when the system is already at or near steady state. At steady state, the P and I components are both very small because the error is very small. If the error suddenly increases it takes a while before the P and I components start kicking in again. However, the D component respond to the sudden change in error and begin compensating immediately. For this reason, it is often said that the D component is responsible for compensating for future error; it sees the error changing and tries to prevent it from changing more.
Because the derivative component responds to changes in the error, it can be problematic in situations where the measured process variable is noisy. This noise can cause the output to become unstable when the D component is utilized in the control algorithm.
PID Controller Tuning
Tuning a PID controller is the process of determining the ideal values for Kp, Ki, and Kd in order to achieve the desired response. In some systems, you may want the control variable to reach the set point as quickly as possible even it if means overshooting the set point. In other cases, overshooting the set point may be unacceptable.
All of this can be controlled by carefully adjusting the tuning coefficients. The tuning process is beyond the scope of this post, but keep an eye out for my next post where I’ll give a real-world example of tuning a homemade temperature controller.
* When I said that an integral means to “accumulate something over time”, that’s not entirely accurate. An integral is actually the accumulation of something with respect to something else; it doesn’t necessarily have to be time. For example, if you take the integral of width with respect to length, you get area.