Article summary
In my previous post on generative art, we used Python’s Turtle library to learn the basics of generative art. In this post, we’ll dive deeper and create a generative art program that uses recursion to produce infinitely complex pieces. This time, we’ll be using p5.js.
Why use recursion?
You might remember recursion from your computer science courses in college and think, “How does this apply to art?” It may seem like a rigid, mathematical concept, but as you can see in the examples below, recursion manifests itself in the natural world. These patterns repeat upon themselves in a beautiful, unique way, and we can use these patterns to inspire our art.

Let’s dive in.
To explore recursion in generative art, we’re going to build a program that draws a tree. Trees, as you know, are inherently recursive data structures used in many computer algorithms, but they’re also naturally-occurring lifeforms with bark and leaves that grow out of the ground. We’ll combine both of our tree definitions in our tree-drawing program.
First off, open up the p5.js web editor. You’ll notice that the project is initialized with some boilerplate code, which sets up a blank canvas with a gray background.
function setup() {
createCanvas(400, 400);
}
function draw() {
background(220);
}
The one modification we’ll make to this boilerplate is adding a call to noLoop inside of setup. By default, p5.js re-runs draw on every frame. This is useful for animated pieces, but since we’re drawing a static image, we can use noLoop to disable this behavior.
function setup() {
createCanvas(400, 400);
noLoop();
}
Next, let’s write the signature for our recursive tree function:
function drawTree(x, y, angle, length) {}
In our function, x and y will represent the coordinates of the base of the tree, angle will denote the angle in radians at which the tree is leaning, and length will denote the length, in pixels, of the tree’s trunk.
Let’s continue with a non-recursive implementation of our function:
function drawTree(x, y, angle, length) {
const [x1, y1] = [x, y];
const x2 = x1 + cos(angle) * length;
const y2 = y1 - sin(angle) * length;
line(x1, y1, x2, y2);
}
Using a bit of trigonometry, this function draws a line starting at (x, y) with an angle and length as specified in the parameters. Note that in p5.js, the origin of the coordinate plane is the top-left corner, so y-coordinates increase in value as you go down the canvas, hence the - in the y2 calculation.
Try calling the drawTree function inside of draw to verify that it works as expected. This invocation, for example, should draw a line starting at the bottom-center of the screen at a 90-degree angle and at a length of 1/2 of the canvas:
drawTree(
width / 2,
height,
PI / 2,
height / 2
);

Add the recursive step.
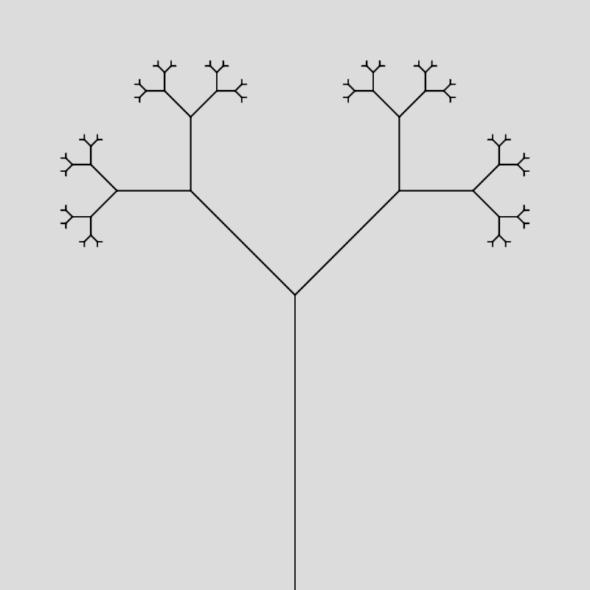
Now let’s add the recursive step to our function. We’ll branch into two sub-trees, one leaning left and one leaning right, each half the length of the previous tree. Of course, since this is a recursive function, we also need to define a base case. We’ll set a minLength of 5 at the top of our program, and stop recursing if length falls below it.
const minLength = 5;
function drawTree(x, y, angle, length) {
const [x1, y1] = [x, y];
const x2 = x1 + cos(angle) * length;
const y2 = y1 - sin(angle) * length;
line(x1, y1, x2, y2);
if (length >= minLength) {
drawTree(x2, y2, angle + PI / 4, length / 2);
drawTree(x2, y2, angle - PI / 4, length / 2);
}
}
With this modification, we get our first tree-like output:
Right now, our program produces the exact same output on every run, which is a little boring. Let’s fix that by moving our inputs to variables and giving them random values in the setup function.
let baseLength;
let minLength;
let lengthRatio;
let angleChange;
function setup() {
createCanvas(400, 400);
noLoop();
baseLength = random(height / 8, height / 2);
minLength = random(1, 10);
lengthRatio = random(0.25, 0.75);
angleChange = random(PI / 32, PI / 3);
}
function draw() {
background(220);
drawTree(width / 2, height, PI / 2, baseLength);
}
function drawTree(x, y, angle, length) {
const [x1, y1] = [x, y];
const x2 = x1 + cos(angle) * length;
const y2 = y1 - sin(angle) * length;
line(x1, y1, x2, y2);
if (length >= minLength) {
drawTree(x2, y2, angle + angleChange, length * lengthRatio);
drawTree(x2, y2, angle - angleChange, length * lengthRatio);
}
}
Re-running our program now, we get results that look much more diverse:

Of course, I promised we were going to take inspiration from real-life trees here, so let’s add some leaves. We’ll add a drawLeaves function with the following signature:
function drawLeaves(x, y) {}
Next, we’ll add a couple more variables to the top of our file, leafDensity and leafColor, and randomize them in setup.
let leafDensity;
let leafColor;
// in setup
leafDensity = random(0, 10);
leafColor = color(
random(0, 255),
random(0, 255),
random(0, 255)
);
Finally, we’ll implement our drawLeaves function and call it in the else clause of our drawTree function, so leaves are only drawn at the end of branches.
function drawTree(x, y, angle, length) {
const [x1, y1] = [x, y];
const x2 = x1 + cos(angle) * length;
const y2 = y1 - sin(angle) * length;
line(x1, y1, x2, y2);
if (length >= minLength) {
drawTree(x2, y2, angle + angleChange, length * lengthRatio);
drawTree(x2, y2, angle - angleChange, length * lengthRatio);
} else {
drawLeaves(x2, y2);
}
}
function drawLeaves(x, y) {
push();
fill(leafColor);
noStroke();
for (let i = 0; i < leafDensity; i++) {
circle(
randomGaussian(x, 10),
randomGaussian(y, 10),
random(2, 5)
);
}
pop();
}
Some special notes about this code:
- The
pushandpopfunctions allow us scope styles like fill and stroke to this particular function call. This allows us to applynoStroketo the leaves while still using the default stroke on the branches. randomGaussianproduces random numbers using a normal (bell-shaped) distribution, unlikerandomwhich uses a uniform distribution. This allows us to make the leaves cluster close to (x,y). Normal distributions are found more commonly in nature than uniform distributions, sorandomGaussianis usually the way to go when you want to mimic nature.
When we run the program now, we get the following results, and with that, our program is done!

It doesn't stop there
Recursion allows us to generate beautiful, complex pieces with just a few lines of code. This tree example only scratches the surface. Below are some of my recent pieces using recursion, to give a few examples of the possibilities:

What will you create?

