If you need an algorithm to solve a complex geometry problem, and you find yourself breaking out your old trigonometry textbook, wait! Vectors might provide a much simpler solution.
vector (noun): A quantity having direction as well as magnitude, esp. as determining the position of one point in space relative to another.
Vector operations can greatly simplify complex geometry problems, especially if what you need is an algorithm to solve a general case, and not just a very specific one-time solution. In fact, if you’re coding something that needs to keep track of positions and/or movement and you’re not using vectors, you’re probably over-complicating things.
Advantages of Using Vectors
- Simple: I find that vectors greatly simplify both the implementation and my understanding of geometrical algorithms.
- Less Trig: Vectors can often help eliminate unnecessary use of trig functions, which are computationally expensive, and I think are harder to conceptualize.
- Robust:Hand-rolled solutions to complex geometry problems often only work if some point is to the left of another, or if the points are sorted by distance, etc… If you stick with the right primitive vector operations, your algorithms will usually “just work” and will often “just work” in any number of dimensions.
Example Problem
Let’s start with a (very contrived) example problem:
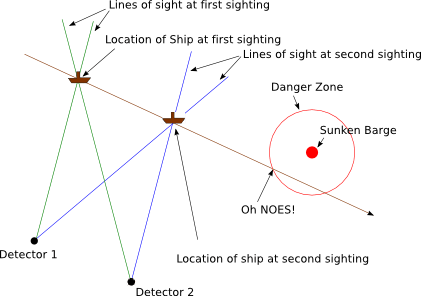
A giant barge recently sank in a busy, shallow harbor. Your company has been hired to build a device to detect if ships coming into the harbor are in danger of hitting the wreckage. Your company has built detectors that can tell what direction a ship is from a detector, but not the distance. You’ve been tasked with writing an algorithm that will triangulate the position of an incoming ship at two different times and determine if the ship’s trajectory will bring it dangerously close to the wreckages. (You did suggest that they just setup a wreck buoy, but they said that would be a terrible example problem for vector math.)
Pretty picture time:
Using the following information:
- The position of the detectors
- The direction of the ship from both detectors at two different times
- The position of the hazard
- The safe distance from the hazard
Construct an algorithm to detect if a ship is in danger if it stays on its current
trajectory, or indicates failure if it’s impossible to deduce from the given information
(this would happen if the ship and the two detectors all lined up)
To be more specific, if we were doing this in C, we’d need the implementation of the following prototype:
// DetectDanger.h
#include "Vector2D.h"
bool Detect_Ship_In_Danger(bool * const in_danger,
Position2D const detector1_pos,
Direction2D const detector1_ship_direction_time1,
Direction2D const detector1_ship_direction_time2,
Position2D const detector2_pos,
Direction2D const detector2_ship_direction_time1,
Direction2D const detector2_ship_direction_time2,
Position2D const hazard_pos,
float const hazard_danger_radius);
Wow, that sounds hard! But hopefully I can show you a few simple primitives that make it easy to solve this problem without any trig at all! This problem can be solved using a combination of just a few simple vector operations. If you’re in a hurry, you can skip to the solution.
Vector Basics
Below is a list of some of the basic vector operations, just to make sure you are aware of them. (These work in any number of dimensions.)
- addition / subtraction
- scalar multiplication
- magnitude (length)
- dot product
- cross product / perpendicular
- rotations (These are an extremely important, useful, and simple operation, but we won’t be using them in this exercise.)
In this post, I’m going to show you how to use some higher-level operations (built from these basic ones) to solve the above problem in a much more elegant way.
And there will be links to code! That you are free to just copy and paste!
A Higher-Level API
We’re going to limit ourselves to just 2 dimensions for the problem at hand, but these operations generalize to N-dimensions.
Vector Representations:
- Position (x, y coordinates)
- Direction (a vector of length 1, a unit vector)
These are both just 2D vectors, and we could just use a single type to represent them all, but I usually try to wrap a generic 2D vector in separate types (that denote their meaning) to prevent me from accidentally mixing them up.
The basics:
- Distance and direction from one position to another
- Position that is a distance and direction from another position
The heavy hitters:
- Position on a line that is closest to another point
- Intersection of line defined by a position and direction, with another line defined by a position and direction
The code for all these operations is here.
The Solution
Given the position of the detectors and the directions from them to the ship, we can use the intersection operation to get the position of the ship at one point in time. And we can do the same thing for the other point in time.
That gives us two points. We can construct a line from that (a position and direction). We can then use the “closest point on a line to another point” operation to get the point along a ship’s current trajectory that it will be the closest to the hazard. Then we can just get the distance between the that point and the hazard and check to see if it’s less than the safe distance.
The implementation is fairly readable:
// DetectDanger.c
#include "DetectDanger.h"
bool Detect_Ship_In_Danger(bool * const in_danger,
Position2D const detector1_pos,
Direction2D const detector1_ship_direction_time1,
Direction2D const detector1_ship_direction_time2,
Position2D const detector2_pos,
Direction2D const detector2_ship_direction_time1,
Direction2D const detector2_ship_direction_time2,
Position2D const hazard_pos,
float const hazard_danger_radius)
{
Position2D ship_pos_at_time1;
Position2D ship_pos_at_time2;
/* I really want a maybe monad here :( */
if ( Vector2D_LineIntersection( &ship_pos_at_time1
, detector1_pos
, detector1_ship_direction_time1
, detector2_pos
, detector2_ship_direction_time1))
{
if (Vector2D_LineIntersection( &ship_pos_at_time2
, detector1_pos
, detector1_ship_direction_time2
, detector2_pos
, detector2_ship_direction_time2))
{
Direction2D const ship_direction = Vector2D_Direction( ship_pos_at_time1
, ship_pos_at_time2 );
Position2D const closest_point =
Vector2D_ClosestPointToLine( ship_pos_at_time2
, ship_direction
, hazard_pos);
*in_danger = Vector2D_Distance(closest_point, hazard_pos) <= hazard_danger_radius;
return true;
}
}
return false;
}
That wasn't too bad! We didn't have to use any trig at all!
And this really just scratches the surface of what you can do with vectors. Rotations are also very easy to represent as vectors (or matrices) and are extremely powerful. (You do need a teeny-weeny bit of trig to convert between rotations and angles and back, but usually only on your inputs and outputs. You can get the rotation to move from one direction to another without using any trig at all.)
You might occasionally still run into a problem where you need to get your hands dirty and solve some trig, but hopfully this should make the majority of cases much easier.