Article summary
On a recent project, I took a list of items and grouped them into categories using a recursive partition function. Today I’ll explain that concept and show you how to implement it in Scala.
As my example, I’ll be categorizing fun, delicious M&M’s by color. (Because, as everyone knows, blues are best and should be saved for last.) For me, this example is nostalgia-inducing as this is a common elementary school activity where I’m from. We can assume M&M colors are mutually exclusive; there’s no overlap between the sets of color A and color B.
What Is a Partition?
Conceptually, a partition is a separation between items. In this case, it means to separate an input group into two smaller groups.
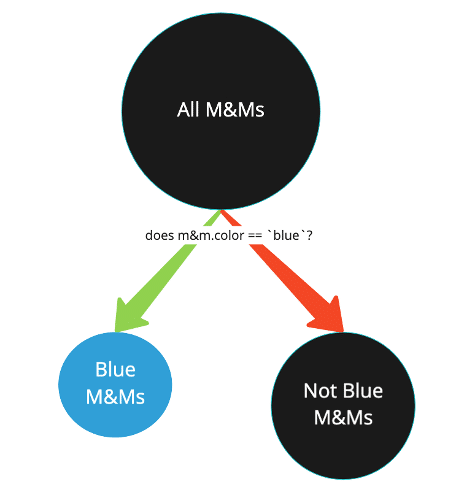
Imagine you’re only interested in separating those wonderful blue M&M’s from the not-blue M&M’s. You need to part the group once:
In Scala, this would look like:
val groups = allTheMAndMs.partition((mAndM: MAndM) => mAndM.color == `blue`)
This partitions all the M&M’s into two groups (or lists):
- Blue M&M’s – All the M&M’s where the conditional is true (color is equal to blue)
- Not Blue M&M’s – All the M&M’s where the conditional is false
If we want to separate all the M&M’s into groups, we need to talk about recursion.
What Is Recursion?
A recursive function is a function that can invoke itself. Our recursive partition function will continue invoking itself until there are no more test functions to use — in our case, no more M&M colors left to check for.
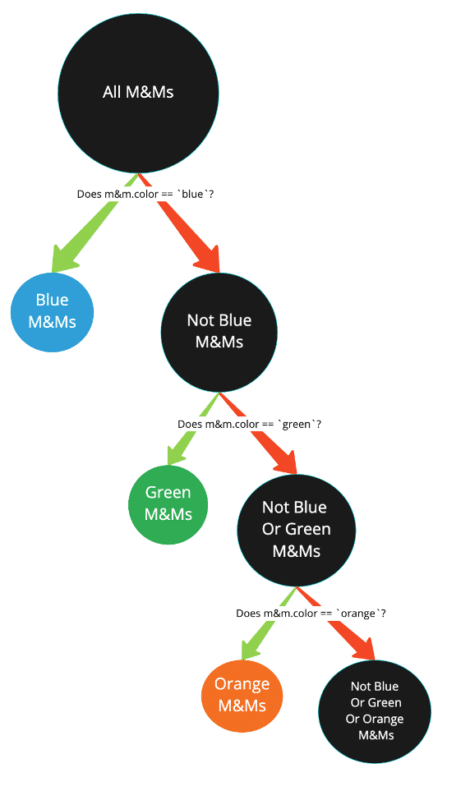
Here’s an implementation of the recursive partition that will group all of the M&M’s by color:
def recursivePartition[A](set: Traversable[A],
partitionFunctions: Map[String, (A) => Boolean],
results: mutable.Map[String, Traversable[A]])
: mutable.Map[String, Traversable[A]] = {
if (partitionFunctions.isEmpty) {
results
} else {
val partitioned = set.partition(partitionFunctions.head._2)
recursivePartition(partitioned._2, partitionFunctions.tail, results += (partitionFunctions.head._1 -> partitioned._1))
}
}
You’ll notice the first parameter, set, is the source set of M&M’s to divide. This will initially be all of the M&M’s, but as the groups continue to be separated, elements already categorized will no longer be in the set.
The second parameter is slightly more complicated; it’s a map of the group name to the expression that tests for belonging to that group. For our example, it would be the following map:
val colorGroups = Map(
"blue" -> ((mAndM: MAndM) => mAndM.color == `blue`),
"green" -> ((mAndM: MAndM) => mAndM.color == `green`),
"yellow" -> ((mAndM: MAndM) => mAndM.color == `yellow`),
"orange" -> ((mAndM: MAndM) => mAndM.color == `orange`)
)
Here, the keys are strings naming the group. The values are the expressions that will resolve to a Boolean when provided an element of the set to partition.
Finally, the third parameter is the map of resultant sets. The keys in that map are the names of the groups, and the values are the lists of items in that set.
It may seem confusing to have a parameter as input that is a result. This is necessary because, in a recursive function, we need to keep track of the partial result when the function runs recursively.
At the beginning of the first partition (for blue), that map will be empty. But when we move on to partitioning to green, the blue entry will be in the results set. That’s because the code fragment results += (partitionFunctions.head._1 -> partitioned._1) adds the key of the current color. And at that point, the list of M&M’s of that color is added to the result map.
Keep in mind, partitioned is a list of two entries; the first is those that match the color, the second those that did not match. This makes the usage of ._1 and ._2 necessary to get the first and second entries.
Snack Time
I hope this example and code sample have been helpful. The one downside of this approach is mutating results by appending entries to it. Unfortunately, I haven’t yet been able to avoid this mutability.
The only thing left to do is snack on those wonderful, perfectly sorted M&M’s. Enjoy!