Writing a game-playing AI is a fun process, but checking for wins or valid moves can be one of the boring aspects of the project. More often than not, it ends up being a sizable chunk of your computation time as well.
Bitboards offer a unique solution to those game checks, although at first look, they may seem like a lot of hand wavy code and “magic constants.” I’ll try to demystify bitboards and put you in a position to use them in your game-playing project.
What Are Bitboards?
At their core, bitboards are another data structure to represent your game’s state. The idea is to store your game’s state in an array of bits. Once in that form, you can leverage bitwise operations to quickly perform operations such as adjacency and intersections.
One major limitation of bitboards is that they can contain only one degree of information: presence or absence. The solution to this problem is to store your full game’s state as a composite of bitboards. When looking at Connect 4, it makes the most sense to store two bitboards: one for each player’s pieces.
Why Use Bitboards?
Bitboards have a few advantages, including speed and storage savings. Most game boards can be represented within 64 bits, which is very lightweight. While games will need a few bitboards to represent the state, a few unsigned ints are very easy on memory usage. Bit manipulations are also optimized at a low level, with most manipulations fitting into one clock cycle.
Applying Bitboards to Connect 4
The best way to grasp this concept is to look at some real examples. In this post, I’m going to walk through some examples applied to Connect 4, with the logic written in Python 3. If you’re not familiar with Connect 4, take a minute to look at the rules. The two aspects that are important to us are the board size (seven spaces wide x six spaces tall) and the goal of putting four pieces in a row to win.
I chose to organize the the board as seven bits tall and seven bits wide. Any bits past those 49 aren’t relevant to us. We count incrementing bottom to top, left to right, as shown below.
6 13 20 27 34 41 48
5 12 19 26 33 40 47
4 11 18 25 32 39 46
3 10 17 24 31 38 45
2 9 16 23 30 37 44
1 8 15 22 29 36 43
0 7 14 21 28 35 42
The height is important for two reasons. The first is that it guides the “constant” that we use to bitshift. Second, we include a buffer of one space on the top of the board to prevent the false positives from the board wrapping around (this may make more sense after I explain the bitshifting). Below is a small graphic showing the two bitboards that correspond to the Connect 4 board.
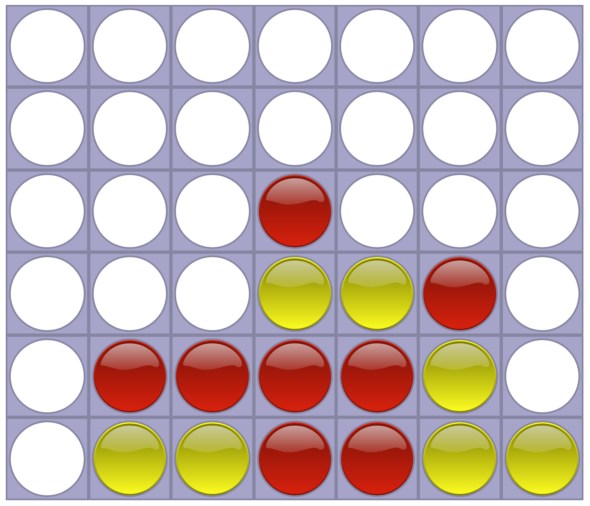
p1_bitboard p2_bitboard
0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 1 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 1 0 0 0 0 1 1 0 0
0 1 1 1 1 0 0 0 0 0 0 0 1 0
0 0 0 1 1 0 0 0 1 1 0 0 1 1
Checking for four in a row with bitboards involves translating the pieces in some direction. To check for X pieces in a row, bitwise AND your starting board with a board translated X-1 spaces in the direction you’re checking.
Four up and down
Translating the pieces within a column is easy; the bit shift is just the distance you want to translate.
Four across
When translating across columns, you need to bitshift by the column height for each space you want to move. In our case, that means we need to bitshift by seven.
Four diagonally
The last case is to translate diagonally. To translate with an ascending diagonal, you would need to shift by the column height plus one to get the pieces one row higher after the shift. Translating a descending diagonal is similar, but you subtract from the column height instead.
Our end goal is to shift three spaces, but we break down the shift into two steps. This ensures that there are four contiguous pieces, instead of two pieces that are four away.
Worked Example
I’m going to work through a quick demo of the process. We’ll use the example above that includes a horizontal win. The code for checking a horizontal solution is below.
temp_bboard = bitboard & (bitboard >> 7)
if(temp_bboard & (temp_bboard >> 2 * 7)):
return True
The check is broken down into two steps. In the first step, we bitwise AND the starting board with a board that has been shifted one column to the right. We do this step to make sure that the middle pieces are present in the four in a row.
Starting bitboard bitboard >> 7 temp_bitboard
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 1 0 0 0 & 0 0 0 0 1 0 0 = 0 0 0 0 0 0 0
0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0
0 1 1 1 1 0 0 0 0 1 1 1 1 0 0 0 1 1 1 0 0
0 0 0 1 1 0 0 0 0 0 0 1 1 0 0 0 0 0 1 0 0
For the next step, we look at two boards. First, we look at the resulting board from Step 1. Then, the same temporary board, with another two column shifts applied to it. We bitwise AND these two boards together to get our final board. If we have any bits present, we’ve found our four pieces in a row.
temp_bboard temp_bboard >> 2 * 7 final bitboard
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 & 0 0 0 0 0 0 0 = 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 1 1 1 0 0 0 0 0 0 1 1 1 0 0 0 0 1 0 0
0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0
I’ve placed the rest of my code to check for a Connect 4 win below. The only major difference between each check is the constant by which the board is shifted.
def find_bb_win(bitboard):
# Check \
temp_bboard = bitboard & (bitboard >> 6)
if(temp_bboard & (temp_bboard >> 2 * 6)):
return True
# Check -
temp_bboard = bitboard & (bitboard >> 7)
if(temp_bboard & (temp_bboard >> 2 * 7)):
return True
# Check /
temp_bboard = bitboard & (bitboard >> 8)
if(temp_bboard & (temp_bboard >> 2 * 8)):
return True
# Check |
temp_bboard = bitboard & (bitboard >> 1)
if(temp_bboard & (temp_bboard >> 2 * 1)):
return True
You should now have a solid understanding of bitboards so you can apply them to your next game-playing project. If you have any questions, comments, or felt like I missed something, please leave a comment below!

